td,dr: A 1100, B1 1300, B2 1800, C1 2000, C2 2300, D1 2200, D2 2700. You needed a 2300 rating to have more than 50% prob of winning a t-shirt and advancing to round 3.
GCJ round 2 took place last weekend. Congratulation to everyone who won the t-shirt and advanced to round 3.
I provide below my estimate of the difficulty of the problems. This is a bit late, and I skipped round 1B and 1C, but I will do a summary of round 1 to catch up.
The data and methods are the same I described in my previous posts, see qualification round and round 1A.
Your feedback is very valuable to increase the quality of the estimates and is very appreciated.
Method 1: The 50% Bucket
Approach and Data
Please see my previous post for an explanation.
Out of around 4'500 participants of GCJ 2, about 2'900 had a CF namesake.
I decided to exclude from the estimate roughly 30 participants with rating below 1000. If you made it this far, your rating doesn't really reflect your ability, so your performance is not a good indicator of the difficulty of the problems.
I also grouped the other participants below 1300 in a single bucket, since there aren't many left.
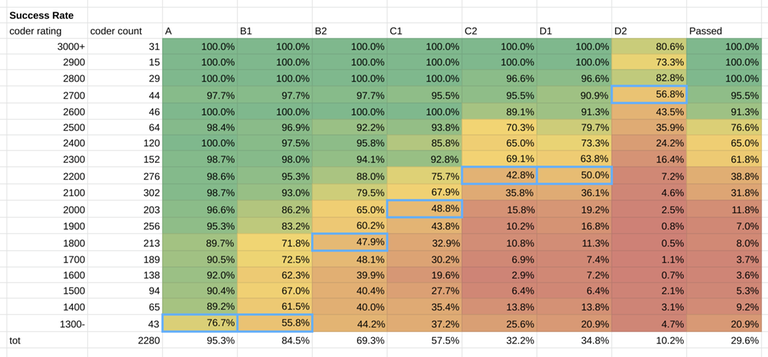
Results
This is the estimate: A 1300, B1 1300, B2 1800, C1 2000, C2 2200, D1 2200, D2 2700.
I think this approach gives reasonable results for most problems, with the exceptions of A and B1. Those two were easy for the majority of the contestants, so this method just places them at the lowest bucket available.
Method 2: Inverse Prob Function
Approach and Data
Again, please see my previous post for more details.
In this round, the average contestant rating was 2020. I tried to imply the difficulty of the problem given the success rate of the contestants close to the average ability ($$$2000 \pm 100$$$ rating), and the results... well, did not improve the estimate by much.
Results based on average contestant's performance
A 1397, B1 1655, B2 1860, C1 1967, C2 2222, D1 2190, D2 2619.
As observed for previous rounds, the approach of inverting the prob function doesn't work well for problems very easy or very difficult for the contestant. For example, the difficulty of B1 is clearly inflated with this approach, and we weren't able to place A at a reasonable level below the 1300 bucket.
Given that the previous buckets method already gives decent results for most problems, can we really learn anything more about the difficulty of the problem using this approach?
I think so. For the easiest and hardest problems, the buckets don't work well. There are not enough contestants around 1000-rating to make enough buckets to estimate the difficulty of problem A. But we can estimate the difficulty of A and B1 based on the performance of the lowest-rated participants. For the hardest problems the buckets seem to work fine so far, but maybe in the coming rounds there will be a similar issue for them.
Adjustments to easy problems based on low rated contestant performance
There are roughly 200 contestants with rating <= 1500. Based on their performance:
A 1,068, B1 1,309.
Much more reasonable.
My Estimate
I put together the two estimates above, and I get this:
A 1100, B1 1300, B2 1800, C1 2000, C2 2300, D1 2200, D2 2700.
What rating did you need to be to pass the round and win a t-shirt? 39% of coders rated 2200 qualified for Round 3. The percentage increases to 62% for 2300 rated participants. You needed to be a Master/close to International Master to have a significant chance to pass. In the table above, right-most column, you can see more details.
What do you think?











I think C1 was easier than B2. I spent over an hour trying to come up with something for B2 and sadly didn't have a clue. C1 was just brute forcing to your answer.
Thanks for the feedback. I am having another look at how many people solved the problems during the contest. Out of 4500 participants, 2630 solved B2, and "only" 2231 solved C1. That's a significant difference. I am trying to put together this statistic with the fact that C1 feels easier. Do you think it's possible that you are just stronger with dp&combinatorics than with number theory, and this made C1 easier for you? After all, with a naive brute force you couldn't pass the case (I think), you needed some sophistication. An alternative could be that many people don't even consider C1 alone, and try to solve C2 directly.
Wow, how accurate my estimation was. The only reason I see D has upper score in your analysis is just because most of non-gm users had no time to solve it.
Nice that we got similar results. Man, I hope you found 4 cheaters
No, nobody has found these cheaters, results are finalized now. I just wasn't good enough to qualify: I solved B in 5 mins after I had written it on sheet of paper, but struggled before it for more than one hour. I forgot to read extra int in A, which cost me couple of minutes. I spent much time debugging my segtree in C, while I could think one more time and solve it just with indices like Mike did. I spent 4 minutes typing D1 and had no time to fix two typos, though this solution came to my mind right after I read this problem. So, next time, I just need more practice.
Nice that I did my estimation only on subjective difficulty, even without seeing number of solvers:)
If it makes feel you any better, I wrote a pretty much the correct solution for C, except that I forgot to take the modulus before returning the answer...
So I passed the first visible test and not the hidden second. When I saw the results, I added two "%=MOD" at the right place, and my code solved both tests. With my penalty time I would have otherwise ended in the top 1000.
As you say, with more practice it will go better