Hi,
I've wrote a solution for problem 883K - Road Widening in C++11 and Golang. C++11 runs in 156 ms, but Golang gets TLE (3000 ms).
C++11: 31844450
Golang: 31844038
Why? Did I do something wrong in the Golang implementation, increasing the time complexity?








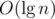 using maps. The second, however, takes more effort. A simple DFS could find and remove the heaviest edge of the cycle, but it would cost
using maps. The second, however, takes more effort. A simple DFS could find and remove the heaviest edge of the cycle, but it would cost 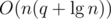 operations in the worst case. Alternatively, it's possible to augment a
operations in the worst case. Alternatively, it's possible to augment a 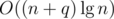 running time.
running time.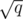 consecutive blocks of
consecutive blocks of 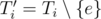 . What does it look like? Sure,
. What does it look like? Sure, 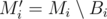 is a minimum spanning forest with at most
is a minimum spanning forest with at most 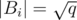 edges. Therefore, a condensation would produce a set
edges. Therefore, a condensation would produce a set 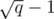 edges. If we use the edges of this MST to initialize and maintain a multiset
edges. If we use the edges of this MST to initialize and maintain a multiset 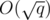 vertices and edges. For the
vertices and edges. For the 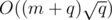 , if we have a fast DSU implementation.
, if we have a fast DSU implementation.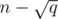 certainly useful edges that will be present for sure in all the MSTs of this block and the at most
certainly useful edges that will be present for sure in all the MSTs of this block and the at most 
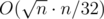 solution appeared! But not for me :( In the whole puzzle, this was the only missing part. All I could think was about an
solution appeared! But not for me :( In the whole puzzle, this was the only missing part. All I could think was about an 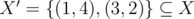 is a solution, because
is a solution, because 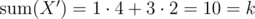 .
.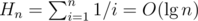 . From that and from the previous bounds, we have
. From that and from the previous bounds, we have 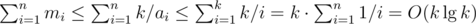 .
.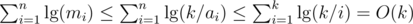 .
. 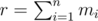 and apply the following dynamic programming.
and apply the following dynamic programming. only if it's possible to find a subsequence from
only if it's possible to find a subsequence from 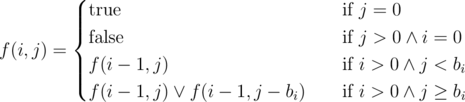
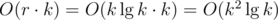 , from Upper Bound 3. The only non-trivial transition is the last: if you can include
, from Upper Bound 3. The only non-trivial transition is the last: if you can include 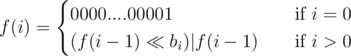
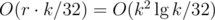 . The non-trivial transition took me some minutes to understand, since I didn't know the precise meaning of this DP. But at this point, I think it's not hard to see that the left shift by
. The non-trivial transition took me some minutes to understand, since I didn't know the precise meaning of this DP. But at this point, I think it's not hard to see that the left shift by 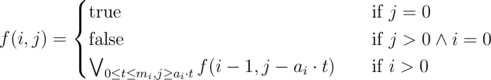
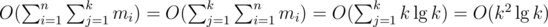 . The only non-trivial transition is the last: all subproblems of the form
. The only non-trivial transition is the last: all subproblems of the form 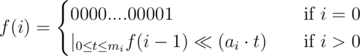
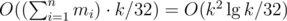 . The non-trivial transition combines all possible amounts
. The non-trivial transition combines all possible amounts 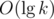 factor. Consider the follwing C++ bottom-up implementation:
factor. Consider the follwing C++ bottom-up implementation: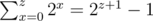 for all non-negative integer
for all non-negative integer 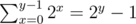 from
from 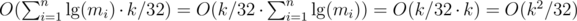 , using Upper Bound 4.
, using Upper Bound 4.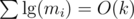 . In the round's problem, we have an even tighter bound. Let me remind you about the first observation of this post:
. In the round's problem, we have an even tighter bound. Let me remind you about the first observation of this post: 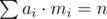
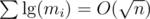 . Hence, the overall complexity using the last algorithm discussed here is
. Hence, the overall complexity using the last algorithm discussed here is 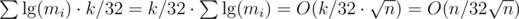 , as
, as 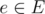 , define
, define  ). I'll explain it one more time, emphasizing how it can be adapted to answer queries about paths on weighted trees (static version, so topology/weight updates are not supported).
). I'll explain it one more time, emphasizing how it can be adapted to answer queries about paths on weighted trees (static version, so topology/weight updates are not supported).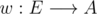 is the weight function. First, we need to define some things, which can all be calculated with a simple DFS:
is the weight function. First, we need to define some things, which can all be calculated with a simple DFS: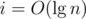 . Then we have
. Then we have 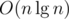 DP states and computing one state costs
DP states and computing one state costs 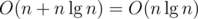 operations (DFS + DP).
operations (DFS + DP).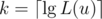 . Set
. Set 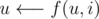 , for
, for 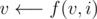 , for
, for 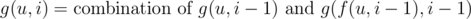
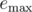 in
in 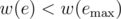 , we improve
, we improve 
