Всем привет!
Как вы знаете, уже третий год подряд финалисты ABBYY Cup собираются летом в московском офисе ABBYY на День открытых дверей. В этом году мне выпала честь написать пост о том, как прошел финал ABBYY Cup 3.0.  Начнем с того, что все дни до 17 июля и после в Москве лил проливной дождь, что совсем не добавляло нам оптимизма: ранее заявленная развлекательная программа сильно зависела от погоды. Похоже, Вселенной было интересно узнать, как пройдет День открытых дверей ABBYY 2013, и она решила не портить этот день осадками : )
Начнем с того, что все дни до 17 июля и после в Москве лил проливной дождь, что совсем не добавляло нам оптимизма: ранее заявленная развлекательная программа сильно зависела от погоды. Похоже, Вселенной было интересно узнать, как пройдет День открытых дверей ABBYY 2013, и она решила не портить этот день осадками : )
Но сюрпризов нам все равно хватило. Автобус с участниками, прибывшими в Москву 16 июля, приехал из кампуса МФТИ в Долгопрудном на целый час раньше. Вот уж никто не ожидал такого подарка от традиционных пробок на Дмитровском шоссе.
И все бы хорошо, если бы остальные участники не должны были приехать к назначенным 10 часам. «Недолго» думая, мы решили развлечь ребят роликом с многообещающим названием «Правда об ABBYY» (или кому-то послышалось нечто другое? : ) В нем в шутливой форме рассказывалось об условиях работы в компании, а также об исследованиях, ведущихся на «самом переднем» крае науки. В 10:40 по московскому времени начался финал ABBYY Cup 3.0! Для меня как для организатора это самое приятное время. Тихо-спокойно идет контест, участники решают задачи… А нам остается с интересом наблюдать за изменениями в таблице результатов соревнования и болеть за любимчиков ; )
В 10:40 по московскому времени начался финал ABBYY Cup 3.0! Для меня как для организатора это самое приятное время. Тихо-спокойно идет контест, участники решают задачи… А нам остается с интересом наблюдать за изменениями в таблице результатов соревнования и болеть за любимчиков ; )
В результате, Egor, опоздавший к началу контеста, подозреваю, даже не завтракавший в этот день, занял первое место! Таким образом, пятерка призеров: Egor, KADR, yeputons, burunduk3, Petr . А полная таблица результатов соревнования здесь.
После тяжелого испытания участники заслужили полноценный горячий обед. Обсуждение задач плавно переместилось в столовую. В этот день мы не могли обойтись без рассказа о компании, поэтому мы попросили выступить наших сотрудников. Сначала с участниками пообщался президент и генеральный директор группы компаний ABBYY Сергей Андреев, а позже главный консультант по продуктам Compreno Александр Костюченко рассказал об исследованиях компании в области компьютерной лингвистики. Далее последовала небольшая экскурсия по офису ABBYY. Некоторые участники уже не первый год приезжают к нам офис.  Так, например, Edvard и aRSeniy быстро нашли xbox и так увлеклись игрой, даже пропустили разбор задач.
Так, например, Edvard и aRSeniy быстро нашли xbox и так увлеклись игрой, даже пропустили разбор задач.
И тут мы подошли к самому главному – награждению. Мы приготовили для ребят сюрприз: все подарки вручал Умный Бобер. Каждый смог прикоснуться к прекрасному: кто-то пожал ему руку, кто-то погладил, а вот Alex_KPR даже обнял.
В качестве развлекательной программы в этом году специально для ребят мы подготовили уникальный квест по центру Москвы! Разбившись на команды, получив задания, фонарики, карты и компасы, в 17 часов участники разбежались в поисках ответов на совершенно непонятные вопросы, которые в конечном итоге должны были привести к финишу. Завершить приключение можно было в любой момент: можно было позвонить нам по специальному номеру и узнать адрес места финиша. 
В процессе подготовки к квесту мы предполагали, что в 21 час все команды устанут и либо найдут место финиша, либо позвонят и сдадутся. Но не тут-то было! В назначенное время никто до финиша еще не дошел, но и сдаваться никто не хотел! Вот это я понимаю, воля к победе! Представьте, каково было команде Mimino.  Специально для него мы подготовили правила на английском языке и предоставили команде переводчика. Думаю, это соревнование для Mimino было куда сложнее любого контеста! А впрочем, аналогичное можно сказать и для всех участников мероприятия : )
Специально для него мы подготовили правила на английском языке и предоставили команде переводчика. Думаю, это соревнование для Mimino было куда сложнее любого контеста! А впрочем, аналогичное можно сказать и для всех участников мероприятия : )
В 22 часа команды потихоньку начали подходить финишу, который к слову, был назначен в одном из местных антикафе. Специально для квеста мы арендовали зал-библиотеку. В нем были собраны книги, старая мебель и музыкальные инструменты, приглушенный свет… Словом, атмосфера была очень романтичная и располагала к поэзии: вот бы сейчас вслух почитать Пастернака. И что же вы думаете? Fefer_Ivan, сидя в винтажном кресле, совершенно непринужденно продекларировал нам одно из стихотворений великого русского поэта XX века.  Который год после Дня открытых дверей ABBYY я еще неделю пребываю в абсолютно влюбленном состоянии во всех спортивных программистов! Но в этот раз я была поражена просто до глубины души. Вот уж, правда, талантливый человек талантлив во всем!
Который год после Дня открытых дверей ABBYY я еще неделю пребываю в абсолютно влюбленном состоянии во всех спортивных программистов! Но в этот раз я была поражена просто до глубины души. Вот уж, правда, талантливый человек талантлив во всем!
Команды постепенно подтягивались, делились впечатлениями и взахлёб рассказывали о своих приключениях. И, как нам показалось, несмотря на большую усталость, были довольными. Дождавшись всех участников и подкрепившись после такой необыкновенной прогулки, мы постепенно стали расходиться: кто в метро, кто к автобусу в Долгопрудный, а кто на работу в офис ABBYY : )
На этом рассказ о Дне открытых дверей ABBYY 2013 заканчивается. Мы хотим сказать огромное спасибо всем участникам мероприятия! Мы очень рады, что есть ребята, которые приезжают к нам не первый год. Не менее приятно познакомиться с новыми лицами. Надеемся, что этот день оставил теплые воспоминания и у вас. До встречи!
https://get.google.com/albumarchive/pwa/114842746780416406882/JInSLJ?authkey=Gv1sRgCLPuzoHEm4X_YQ
Альбом с фотографиями есть в ВКонтакте.









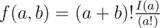 , где
, где 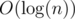 значений
значений 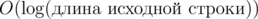 . Теперь рассмотрим некоторый суффикс исходной строки. Мы знаем его LCP с предыдущим суффиксом. Это будет нижняя граница на длину этого суффикса. Заметим, что число вхождений некоторого префикса рассматриваемого суффикса монотонно зависит от длины этого префикса. Поэтому, для каждого правила можно бинарным поиском определить, какой может быть минимальная и максимальная длина префикса, чтобы он подходил под правило. После чего необходимо просто пересечь все полученные интервалы.
. Теперь рассмотрим некоторый суффикс исходной строки. Мы знаем его LCP с предыдущим суффиксом. Это будет нижняя граница на длину этого суффикса. Заметим, что число вхождений некоторого префикса рассматриваемого суффикса монотонно зависит от длины этого префикса. Поэтому, для каждого правила можно бинарным поиском определить, какой может быть минимальная и максимальная длина префикса, чтобы он подходил под правило. После чего необходимо просто пересечь все полученные интервалы.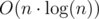 .
.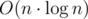 и обрабатывает один запрос за
и обрабатывает один запрос за  . Сложность такого решения составляет
. Сложность такого решения составляет 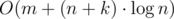 .
.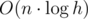 для дерева отрезков или
для дерева отрезков или 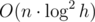 для бинарного поиска и дерева Фенвика. Заметим, что большой разницы в скорости работы этих решений нет за счет скрытых констант при подсчете сложности.
для бинарного поиска и дерева Фенвика. Заметим, что большой разницы в скорости работы этих решений нет за счет скрытых констант при подсчете сложности. .
.
