Problem statement: Given a complete bipartite graph KN, N with weights Wuv assigned to each edge uv, find a perfect matching with minimal sum of edge weights among all perfect matchings.
Is there any easy to code polynomial algorithm for this problem? I know an easy way to solve it using subset dp in O(N22N), and i also think that it is possible to modify the Hungarian Algorithm to solve this problem. But is there any easier algorithm considering it is always a complete bipartite graph? I don't care too much about the time complexity as long as it is polynomial.
Thanks in advance!








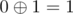 and
and 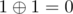 . This trick is really useful and is used in a lot of algorithms like binary heap and iterative segment tree.
. This trick is really useful and is used in a lot of algorithms like binary heap and iterative segment tree.
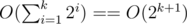 for matchings, which i think is always small but still relevant.
for matchings, which i think is always small but still relevant.
