Sorry for the long wait. These problems were brought to you by Esomer, danx, dutin, jay_jayjay, oursaco, superhelen, thehunterjames, willy108, and TheYashB. Also, massive thanks to omeganot for his unofficial editorial (which was posted a lot sooner than ours).
Novice A/Advanced A: It's Time to Submit
Both "YES" and "NO" are consistent answer (as long as exactly one of them is the answer).
If you print "YES" and get AC, you are getting AC by printing the sample output.
If you print "NO" and get AC, you are getting AC by not printing the sample output.
Never assume just because the carrot is big ... the sample output is correct.
print("NO")
Novice B: A Bit of Monkeying
Under what conditions do the bitwise AND of all the elements in the array equal the bitwise OR?
The bitwise AND is equal to the bitwise OR if and only if all the elements in the array are equal.
Necessary: Consider some bit $$$2^i$$$, and let $$$cnt_i$$$ denote the number of numbers with that bit ON. If $$$cnt_i = 0$$$, then both the total bitwise AND and the total bitwise OR will have bit $$$2^i$$$ OFF. If $$$cnt_i = n$$$, then both the total bitwise AND and the total bitwise OR will have bit $$$2^i$$$ ON. Otherwise, the bitwise OR will be $$$1$$$, and the total bitwise AND will be $$$0$$$. So only if $$$cnt_i = 0$$$ or $$$cnt_i= n$$$ for all $$$i$$$, the bitwise AND and the bitwise OR will be equal. For $$$cnt_i = 0$$$ or $$$cnt_i = n$$$ for all numbers, all the values must be the same (as for each bit you know whether or not there are $$$0$$$ or $$$n$$$ occurrences of that bit).
Sufficient: $$$x | x = x$$$ and $$$x \& x = x$$$ for any nonnegative integer $$$x$$$. This is because for any bit, $$$0 | 0 = 0$$$, $$$0 \& 0 = 0$$$, $$$1 | 1 = 1$$$, and $$$1 \& 1 = 1$$$. To evaluate the total bitwise AND (and total bitwise OR), we can take out $$$a_1$$$ and $$$a_2$$$ and replace them with their bitwise AND (or bitwise OR), but as $$$a_1 = a_2$$$, we can replace it with $$$a_1$$$. We can continue this until only 1 number is left. In both situations, the bitwise AND and bitwise OR are equal to $$$a_1$$$, and therefore they are the same.
The total bitwise AND and the total bitwise OR are the same iff all the elements are the same (read hint 2).
Let's call a value $$$v$$$ good if it is possible to make all the elements equal to $$$v$$$ after some amount of operations. $$$v$$$ must contain $$$O$$$ as a submask where $$$O$$$ is the bitwise $$$O$$$ of all the elements in the array. This is true because, for any bit that is ON in any element in the original array, that bit will still be ON after the operation is applied. In turn, any bit that is ON $$$v$$$ that is not ON in $$$O$$$ must not have been ON in any of the elements in the array (otherwise $$$O$$$ would have that bit ON as well). This means the best value of $$$v$$$ to pick is $$$O$$$. To minimize the number of operations used, we should set all the elements to be $$$O$$$, this can be done in $$$1$$$ operation per element (that isn't $$$O$$$ already). So the answer for the first monkey is $$$n - \text{# } O \text{ in } a_{1 \dots n}$$$.
A similar logic applies for $$$A$$$ where $$$A$$$ is the total bitwise AND of all the elements in the array and the bits that are off.
So the final answer is to compare the number of occurrences of $$$O$$$ and $$$A$$$ in the array. $$$or$$$ if $$$O$$$ occurs more, $$$and$$$ if $$$A$$$ occurs more, or $$$sad$$$ otherwise.
Time complexity: $$$O(n)$$$, $$$O(n \log n)$$$, or $$$O(n \log a_i)$$$.
#include <iostream>
#include <vector>
#include <map>
using namespace std;
int main(){
cin.tie(0) -> sync_with_stdio(0);
int T; cin >> T;
while(T--){
int n;
cin >> n;
vector<int> arr(n);
map<int, int> cnt;
for(int&x : arr){
cin >> x;
cnt[x]++;
}
int or_sum = arr[0], and_sum = arr[0];
for(int i = 1; i<n; i++){
or_sum = or_sum|arr[i];
and_sum = and_sum&arr[i];
}
if(cnt[or_sum] == cnt[and_sum]){
cout << "sad\n";
}else if(cnt[or_sum] > cnt[and_sum]){
cout << "or\n";
}else{
cout << "and\n";
}
}
}
Novice C: Alternet Is Cheating
It is optimal for each of the friends to try to defeat the first real participant that they encounter, so we can use a greedy algorithm.
We simulate the tournament directly, using friends to defeat real participants whenever possible and keeping track of participants who have already defeated a real participant (We choose friends who can still snipe someone over friends who can't).
// {{{1 my template
extern "C" int __lsan_is_turned_off() { return 1; }
#include <bits/stdc++.h>
using namespace std;
#include <tr2/dynamic_bitset>
using namespace tr2;
#include <ext/pb_ds/assoc_container.hpp>
#define ll long long
#define inf 0x3f3f3f3f
#define infl 0x3f3f3f3f3f3f3f3fll
#include <assert.h>
#ifdef DEBUG
#define dprintf(args...) fprintf(stderr,args)
#endif
#ifndef DEBUG
#define dprintf(args...) 69
#endif
#define all(x) (x).begin(), (x).end()
// 1}}}
struct { template<typename T> operator T() { T x; cin>>x; return x; } } in;
int main()
{
int tt = in;
for(int ttn=0;ttn<tt;ttn++)
{
int n=in;
vector<char> a(2*n-1);
for (int i=0;i<n;i++) a[i+n-1] = in;
// A is alternet
// R is orz person
// F is friend
// P is friend but already chosen
for(int i=n-2;~i;i--) {
int x = a[i*2+1], y = a[i*2+2];
char& z = a[i];
if (x == 'A')
z = y=='R'? 'R' : 'A';
else if (y == 'A')
z = x=='R'? 'R' : 'A';
else if (x == 'F')
z = y=='R'? 'P' : 'F';
else if (y == 'F')
z = x=='R'? 'P' : 'F';
else if (x == 'R' || y == 'R')
z = 'R';
else z = 'P';
}
printf("%s\n", a[0] == 'A'? "Yes" : "No");
}
}
Novice D: Haagandaz is Justice
How many "days" will pass at most?
Another way to view the problem is this: "Set the first $$$F(1)$$$ numbers to be $$$T$$$, then set the next $$$F(2)$$$ numbers to be $$$K$$$, then set the next $$$F(3)$$$ numbers to be $$$T$$$ ..." where $$$F(x)$$$ is the $$$x$$$'th Fibonacci number ($$$F(1) = 1$$$ and $$$F(2) = 2$$$).
The Fibonacci sequence grows very quickly (approximately exponentially), so within $$$85$$$ terms the $$$10^{18}$$$'th ice cream will be covered. So we can simulate the process with a brute force, figuring out which ice creams were eaten on day $$$i$$$. Finally, we can check if the day we ate a certain ice cream is odd or even to determine the answer.
The time complexity is $$$O(n \log x_i)$$$.
#include <iostream>
using namespace std;
int answer(long long x){
long long a = 1, b = 1;
long long total = 0;
int turns = 0;
while(total < x){
total += a;
turns++;
a += b;
b = a - b;
}
return turns;
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
int n;
cin >> n;
for(int i = 1; i<=n; i++){
long long a; cin >> a;
int t = answer(a);
cerr << t << "\n";
if(t%2 == 1){
cout << "T";
}else{
cout << "K";
}
}
}
Novice E/Advanced B: Richard Lore
There is one original array $$$a$$$ such that after applying the first $$$m$$$ operations, it will become sorted.
Let $$$b_{1 \dots n}$$$ be the only way to arrange the elements in $$$a$$$ such that after applying all the swaps, $$$b_{1 \dots n}$$$ becomes sorted. The question then splits into two parts:
Obtaining $$$b$$$
Checking if $$$a = b$$$.
So to obtain $$$b$$$, we can sort $$$a$$$ and apply the swaps in reverse order. This is because if we apply the swaps (in the correct order) from $$$b$$$, it will end up as the sorted version of $$$a$$$.
Then to check if $$$a = b$$$, we can maintain a counter for what indices $$$i$$$ $$$a_i = b_i$$$. We can check this for $$$a$$$ and $$$b$$$ initially, and for every query, at most $$$2$$$ indices changed. So we can manually change the counter based on that "small" change. Then the answer to every query is $$$Y$$$ if the counter shows that $$$n$$$ indices are the same across $$$a$$$ and $$$b$$$ or $$$N$$$ otherwise.
The final complexity is $$$O(n + m + q)$$$. It turns out that just comparing $$$a = b$$$ when $$$a$$$ and $$$b$$$ are both vectors can pass in C++. I guess the bounds were too loose/test data wasn't strong enough.
#include <iostream>
#include <utility>
#include <algorithm>
#include <vector>
using namespace std;
int main(){
cin.tie(0) -> sync_with_stdio(0);
int n, m, q;
cin >> n >> m >> q;
vector<int> p(n);
vector<pair<int, int>> arr(m);
for(int i = 0; i<n; i++){
cin >> p[i];
}
for(int i = 0; i<m; i++){
int a, b;
cin >> a >> b;
a--, b--;
arr[i] = pair(a, b);
}
vector<int> srt(n);
for(int i = 0; i<n; i++){
srt[i] = p[i];
}
sort(srt.begin(), srt.end());
reverse(arr.begin(), arr.end());
for(auto [a, b] : arr){
swap(srt[a], srt[b]);
}
int cnt = 0;
for(int i = 0; i<n; i++){
if(srt[i] == p[i]) cnt++;
}
string ans;
for(int i = 0; i<q; i++){
int a, b;
cin >> a >> b;
a--, b--;
cnt -= (srt[a] == p[a]);
cnt -= (srt[b] == p[b]);
swap(p[a], p[b]);
cnt += (srt[a] == p[a]);
cnt += (srt[b] == p[b]);
if(cnt == n) ans.push_back('Y');
else ans.push_back('N');
}
cout << ans << "\n";
return 0;
}
Novice E/Advanced C: Unique Subsequences
Consider two equal subsequences (by character) that differ by exactly $$$1$$$ index chosen. How can you determine if two such subsequences exist?
If for all indices $$$i$$$, there is no other $$$j$$$ such that $$$abs(i - j) \leq n - k$$$ and $$$s_i = s_j$$$ then all subsequences are unique.
We only care about subsequences that differ by exactly $$$1$$$ index chosen, since if more than $$$1$$$ were taken, we can just switch some of them to be the same without affecting the fact that all the subsequences are not unique.
Say we took two subsequences $$$a$$$ and $$$b$$$ such that they are different (WLOG $$$a_i \leq b_i$$$). We know that $$$a_1 \geq 1, a_2 \geq 2 \dots a_k \geq k$$$ and that $$$b_k \leq n, b_{k-1} \leq n-1, \dots b_1 \leq n - k + 1$$$. This means $$$s_{a_i} = s_{b_i}$$$ and $$$b_i - a_i \leq (n - k + i) - (i)$$$. $$$b_i - a_i \leq n - k$$$. So it is necessary that in the subsequences there exists some $$$i$$$ such that $$$b_i - a_i \leq n - k$$$. (necessary)
Assume WLOG $$$i < j$$$ and we picked $$$s_{a_1}, s_{a_2} \dots s_{a_{x-1}}, s_{a_{x}}, s_{a_{x+1}} \dots s_{a_{k-1}}, s_{a_k}$$$ for some $$$a_1 < a_2 < a_3 \dots a_k$$$ and $$$a_x = i$$$. We are going to try and change $$$a_x = j$$$. We know that $$$a_1 \geq 1, a_2 \geq 2, \dots a_{x} \geq x$$$. We also know that $$$a_k \leq n, a_{k-1} \leq n-1, \dots a_{x} \leq n - (k - x)$$$. So this means that $$$x \leq a_x \leq n - (k - x)$$$. So at the worse case $$$i = x$$$ and $$$j = n - (k - x)$$$, $$$abs(i - j) = j - i = n - (k - x) - x = n - k$$$. So there must be two equal elements with distance at most $$$n - k$$$ for there to exist for it to be possible for two subsequences that are the same (sufficient).
We can check this condition with a for loop in $$$O(n)$$$ or $$$O(\alpha n)$$$ where $$$\alpha$$$ is the alphabet size ($$$26$$$).
#include <iostream>
#include <string>
#include <array>
using namespace std;
int main(){
cin.tie(0) -> sync_with_stdio(0);
int T;
cin >> T;
while(T--){
int n, k;
cin >> n >> k;
string s;
cin >> s;
array<int, 26> occ;
occ.fill(-1);
int work = 1;
for(int i = 0; i<n; i++){
char c = s[i];
if(occ[c-'a'] != -1){
if((i - occ[c-'a']) <= (n - k)){
work = 0;
}
}
occ[c-'a'] = i;
}
if(work) cout << "Yes\n";
else cout << "No\n";
}
}
Novice G/Advanced D: Sleepy Pandas
The concatenation of $$$a$$$ and $$$b$$$ is $$$a \cdot 10^{\lceil \log_{10}(a) \rceil} + b$$$.
$$$10^{\lceil \log_{10}(x) \rceil}$$$ is the smallest power of $$$10$$$ no less than $$$x$$$.
For a fixed $$$b$$$, how can we count all the valid $$$a$$$ such that the concatenation is divisible by $$$K$$$?
Consider reading the two hints as the solution goes off of them.
Let's enumerate $$$tp$$$ as the power of ten which is $$$10^{\lceil \log_{10}(j) \rceil}$$$. For $$$a \cdot tp + b \equiv 0 \pmod{K}$$$, we need $$$a \cdot tp \equiv -b \pmod{K}$$$. So we can store a map of all the frequencies of $$$a \cdot tp \text{ mod } K$$$, and for each $$$b$$$, add the frequency of $$$-b \text{ mod } K$$$. It is important to only add for $$$b$$$ such that $$$10^{\lceil \log_{10}(j) \rceil} = tp$$$.
The final time complexity is $$$O(n \log x_i \log n)$$$.
def ceil10(x):
y = 1
while y <= x:
y *= 10
return y
assert ceil10(0) == 1
assert ceil10(9) == 10
assert ceil10(19) == 100
assert ceil10(1e9) == 10000000000
T = int(input())
for _ in range(T):
N, K = map(int, input().split())
a = list(map(int, input().split()))
cnt = 0
for tp in [10**p for p in range(1, 10)]: # Similar to 1e10 in C++
mp = {}
for i in range(N):
x = (K - tp % K * a[i] % K) % K # -a[i]*tp
mp[x] = mp.get(x, 0) + 1
for i in range(N):
if ceil10(a[i]) != tp:
continue
x = (K - tp % K * a[i] % K) % K # -a[i]*tp
mp[x] -= 1
cnt += mp.get(a[i] % K, 0)
mp[x] += 1
print(str(cnt))
Novice H: Afterimages
$$$abs(a - b) = \max(a, b) - \min(a, b)$$$
Consider the odd and even indices separately.
Let $$$ao$$$ and $$$ae$$$ denote the elements in $$$a$$$ in odd and even indices respectively (both should have length $$$\frac{n}{2}$$$.
Define $$$bo$$$ and $$$be$$$ similarly for $$$b$$$.
Also for the sake of simplicity, lets duplicate each array (for instance $$$ao_{i} = ao_{i + \frac{n}{2}}$$$.
Let's find the answer for each of the $$$4$$$ parts separately. To find the greatest awkwardness for $$$ao_i$$$, we need to find the max value in $$$bo_{i \dots i + k}$$$. This can be done with a sliding window in $$$O(n)$$$ or $$$O(n \log n)$$$.
A similar strategy works for $$$bo$$$ and $$$be$$$.
Let $$$p'$$$ denote the reverse of $$$p$$$. We can use the same algorithm for $$$bo'$$$ and $$$ao'$$$ and for $$$be'$$$ and $$$ae'$$$. The total complexity is $$$O(n)$$$ or $$$O(n \log n)$$$ depending on how you did the sliding window.
#include <iostream>
#include <vector>
#include <set>
#include <utility>
#include <algorithm>
#include <cmath>
#include <iterator>
#define all(x) x.begin(), x.end()
using namespace std;
long long answer(vector<int> A, vector<int> B, int steps){
//same parity
int n = A.size();
multiset<int> ms;
for(int i = 0; i<steps; i++){
ms.insert(A[i]);
}
long long ret = 0;
for(int i = 0; i<B.size(); i++){
auto [mn, mx] = make_pair(*ms.begin(), *prev(ms.end()));
ret += max(B[i] - mn, mx - B[i]);
ms.erase(ms.lower_bound(A[i%n]));
ms.insert(A[steps%n]);
steps++;
}
return ret;
}
void solve(){
int n; cin >> n;
long long k; cin >> k;
k--;
vector<int> A(n), B(n);
vector<int> Ao, Ae, Bo, Be; //A odd, A even, etc
for(int i = 0; i<n; i++){
cin >> A[i];
if(i%2 == 0) Ae.push_back(A[i]);
else Ao.push_back(A[i]);
}
for(int i = 0; i<n; i++){
cin >> B[i];
if(i%2 == 0) Be.push_back(B[i]);
else Bo.push_back(B[i]);
}
auto ansAo = answer(Bo, Ao, min(k+1, (long long)n/2));
auto ansAe = answer(Be, Ae, min(k+1, (long long)n/2));
reverse(all(Ao)); reverse(all(Ae));
reverse(all(Bo)); reverse(all(Be));
auto ansBo = answer(Ao, Bo, min(k+1, (long long)n/2));
auto ansBe = answer(Ae, Be, min(k+1, (long long)n/2));
cout << ansAo + ansBo + ansAe + ansBe << "\n";
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
int T; cin >> T;
for(int i = 0; i<T; i++){
solve();
}
return 0;
}
Novice I/Advanced F: Another Bitwise Problem
I drank the solution last night. Refer to the solution code for now until I titrate another one.
#include <bits/stdc++.h>
using namespace std;
#define int int64_t
typedef vector<int> vi;
typedef pair<int, int> pi;
typedef vector<pi> vpi;
#define all(x) x.begin(), x.end()
#define pb push_back
#define endl '\n'
#define f first
#define s second
#define FOR(i, a, b) for (int i = (a); i < (b); i++)
template <class T> istream &operator>>(istream& in, vector<T> &v) {for (auto& i : v) in >> i; return in;}
#ifdef HORI
#include "../../lib/debug.h"
#else
#define dbg(...)
#endif
const int M = 18;
signed main() {
ios::sync_with_stdio(0); cin.tie(0);
int n, l, r; cin >> n >> l >> r;
vi a(n); cin >> a;
vpi s;
FOR(b, 0, M) {
int z = 0, o = 0;
FOR(i, 0, n) {
if (a[i] & (1 << b)) {
o++;
} else {
z++;
}
}
s.pb({z * (1 << b), o * (1 << b)});
}
int ans = 0;
set<int> st;
FOR(mask, 0, (1 << M)) {
int sum = 0;
FOR(i, 0, M) {
if ((1 << i) & mask) {
sum += s[i].f;
} else {
sum += s[i].s;
}
}
st.insert(sum);
}
for (int sum : st) {
int nr = r - sum;
int nl = l - sum;
if (nr >= 0) {
ans += nr / ((1 << M) * n) + 1;
}
if (nl > 0) {
ans -= (nl - 1) / ((1 << M) * n) + 1;
}
}
cout << ans << endl;
}
Novice J: Everyone Loves Threes Magic (Easy Version)
Solve each test case in $$$O(R - L)$$$ time.
Let $$$f(i)$$$ be $$$0$$$ if $$$i$$$ is not divisible by $$$3$$$ or the number of $$$3$$$'s in the base-$$$10$$$ representation of $$$i$$$ otherwise.
As there are $$$(R - i + 1)(L - i + 1)$$$ choices of $$$l$$$ and $$$r$$$ such that $$$L \leq l \leq i \leq r \leq R$$$.
Can you simplify the formula?
We can rewrite the terms as
We can consider the sum to be $$$A \sum_{i = L}^{r} f(i) + B \sum_{i = L}^{R} if(i) + C \sum_{i = L}^{R} i^2f(i)$$$ where $$$A$$$, $$$B$$$, and $$$C$$$, are constants only dependant on $$$L$$$ and $$$R$$$. In particular (in the $$$3$$$rd hint), $$$A = (R + 1)(- L + 1), B = (-(-L + 1) + (R + 1)), C = -1$$$.
We can precompute prefix sums on $$$\sum f(i)$$$, $$$\sum if(i)$$$, and $$$\sum i^2f(i)$$$ to evaluate those parts of the sum in constant time. The final complexity is $$$O(R)$$$ precomputation and $$$O(1)$$$ per test case. Be careful of integer overflow.
#include <iostream>
using namespace std;
#define ll long long
const int MX = 1e6+10;
const ll mod = 998244353;
ll pre[MX], prelin[MX], presq[MX];
int f(int x){
if(x == 0) return 0;
return (x%10 == 3) + f(x/10);
}
//(r - i + 1)(i - l + 1)f(i)
//(r+1)(-l+1)sum[i] + (-(-l+1) + r+1)*i*sum[i] + -i^2*sum[i]
void solve(){
int l, r;
cin >> l >> r;
ll a = 1ll*(r+1)*(1+mod-l)%mod*(pre[r] + mod - pre[l-1])%mod;
ll b = 1ll*(mod + -(-l + 1) + r + 1)*(prelin[r] + mod - prelin[l-1])%mod;
ll c = 1ll*(mod -1)*(presq[r] + mod - presq[l-1])%mod;
cout << (a + b + c)%mod << "\n";
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
for(int i = 1; i<=(int)(1e6); i++){
if(i%3 == 0){
int F = f(i);
pre[i] = F;
prelin[i] = F*i;
presq[i] = 1ll*F*i*i%mod;
}
pre[i] += pre[i-1];
prelin[i] += prelin[i-1];
presq[i] += presq[i-1];
if(prelin[i] >= mod) prelin[i] %= mod;
if(presq[i] >= mod) presq[i] %= mod;
}
int T; cin >> T;
while(T--){
solve();
}
return 0;
}
Novice K/Advanced E: Another Ordering Problem
Each edge can be treated as being undirected
Consider each connected component separately.
Each connected component is a tree with an edge. How would you solve it on a tree without the extra edge?
If there was no extra edge, this is an MIS (maximum independent set) on a tree. This can be done with a tree dp (dynamic programming) of $$$dp[u][0/1]$$$ denotes the max sum for the subtree of node $$$u$$$ with $$$0/1$$$ denoting whether or not we took node $$$u$$$ or not.
$$$dp[u][0] = \sum\limits_{v \text{ is adjacent to }u} \max(dp[v][0], dp[v][1])$$$
$$$dp[u][0] = a_u + \sum\limits_{v \text{ is adjacent to }u} dp[v][0]$$$
For each connected component, we can pick some edge $$$(r, p)$$$ such that the graph such that it becomes a tree. Let's root the tree at $$$r$$$. The only change this extra edge makes to the answer is that we cannot take both nodes $$$p$$$ and node $$$r$$$ at the same time.
So this motivates adding another flag to the dp to check if we took node $$$u$$$ or not. Let $$$dp[u][0/1][0/1]$$$ denote the best answer for the subtree of node $$$u$$$ with the first flag checking if we took node $$$u$$$ or not and the second flag checking if we took node $$$p$$$ (if $$$p$$$ isn't in the subtree of node $$$u$$$, $$$dp[u][0/1][1]$$$ isn't defined). You can check the code below for transitions.
The total time complexity is $$$O(n)$$$.
The code may look long but the transitions are almost all the same.
#include <iostream>
#include <cmath>
#include <utility>
#include <cassert>
#include <algorithm>
#include <vector>
#include <array>
#define sz(x) ((int)(x.size()))
#define all(x) x.begin(), x.end()
#define pb push_back
using ll = long long;
const int MX = 2e5 +10, int_max = 0x3f3f3f3f;
using namespace std;
int par[MX];
ll dp[MX][2][2]; //took/not took | took good node/took bad node
vector<int> adj[MX];
int cost[MX], vis[MX], dsu[MX];
int n;
int find(int u){
if(dsu[u] != u) dsu[u] = find(dsu[u]);
return dsu[u];
}
void gpar(int u, int p){ //generate the parents
par[u] = p;
for(int v : adj[u]){
if(v == p) continue;
gpar(v, u);
}
}
void gvis(int u){ //mark all the ancestors of a node
if(u == 0) return ;
vis[u] = 1;
gvis(par[u]);
}
void dfs(int u, int p, int bad){
for(int v : adj[u]){
if(v == p) continue;
dfs(v, u, bad);
}
if(vis[u] == 0){
ll sum0 = 0, sum1 = 0;
for(int v : adj[u]){
if(v == p) continue;
sum0 += max(dp[v][0][0], dp[v][1][0]);
sum1 += dp[v][0][0];
}
dp[u][0][0] = sum0;
dp[u][1][0] = sum1 + cost[u];
}else if(u == bad){
ll sum0 = 0, sum1 = 0;
for(int v : adj[u]){
if(v == p) continue;
sum0 += max(dp[v][0][0], dp[v][1][0]);
sum1 += dp[v][0][0];
}
dp[u][0][0] = sum0;
dp[u][1][1] = sum1 + cost[u];
}else{
for(int j = 0; j<2; j++){
ll sum0 = 0, sum1 = 0;
for(int v : adj[u]){
if(v == p) continue;
if(vis[v]){
sum0 += max(dp[v][0][j], dp[v][1][j]);
sum1 += dp[v][0][j];
}else{
sum0 += max(dp[v][0][0], dp[v][1][0]);
sum1 += dp[v][0][0];
}
}
dp[u][0][j] = sum0;
dp[u][1][j] = sum1 + cost[u];
}
}
}
ll go(pair<int, int> bad){
auto [u, v] = bad;
if(u == v) return 0;
gpar(u, 0);
gvis(v);
dfs(u, 0, v);
return max({dp[u][0][0], dp[u][0][1], dp[u][1][0]});
}
int main(){
cin >> n;
for(int i = 1; i<=n; i++) dsu[i] = i;
vector<pair<int, int>> bad;
for(int i =1; i<=n; i++){
cin >> cost[i];
int j;
cin >> j;
if(find(i) == find(j)){
bad.push_back({i, j});
}else{
dsu[find(i)] = find(j);
adj[i].pb(j);
adj[j].pb(i);
}
}
ll ans = 0;
for(auto p : bad){
ans += go(p);
}
cout << ans << "\n";
}
Novice L/Advanced H: Gaslighting
Let $$$lcp(i, j)$$$ denote the longest common prefix of the suffixes starting at $$$s_i$$$ and $$$s_j$$$. This can also be seen as the maximum number of characters that can be extended from $$$s_i$$$ and $$$s_j$$$ such that both substrings are still equal.
Let $$$len = r - l + 1$$$. Note that an answer of $$$l' \ r'$$$ can also be seen as $$$l' \ l' + len$$$.
For a fixed $$$l$$$, $$$l'$$$ will provide an answer for an interval of $$$len$$$. At some $$$len$$$, there will be no different characters between $$$s_{l \dots l + len}$$$ and $$$s_{l' \dots l' + len}$$$. At some larger $$$len$$$, there will be more than one different character.
Then for a fixed $$$l$$$, the interval of len for which $$$l'$$$ is a valid answer is (define $$$c = lcp(l, l')$$$) $$$[c + 1, lcp(l + c + 1, l' + c + 1)]$$$. This is because for any $$$len < c + 1$$$, there are $$$0$$$ differences between $$$s_{l \dots l + len}$$$ and $$$s_{l' \dots l' + len}$$$. More importantly, however, is that $$$lcp(l + c + 1, l' + c + 1)$$$ denotes the longest common prefix after one error is accounted for (hence the $$$+c + 1$$$. So any $$$len > lcp(l + c + 1, l' + c + 1)$$$ will have at least $$$2$$$ differences.
Use these facts to make an $$$O(n^2 \log n + q)$$$ solution.
For each $$$l$$$, we can first generate all the intervals of $$$len$$$ for each $$$l'$$$. Then we can do a sweep where we maintain a set of "active" intervals for each $$$len$$$. At $$$len = c+1$$$, we can insert $$$l'$$$ to our active set, then at $$$len = lcp(l + c + 1, l' + c + 1) + 1$$$, we can remove it from our set. For each $$$len$$$, we check if any interval is active, and if so, store its $$$l'$$$ as a valid answer for a query with that $$$l$$$ and $$$len$$$.
vector<int> process(vector<array<int, 3>> arr){ //stores the intervals as [lo, hi, l']
set<int> pres;
vector<vector<int>> events(n+2);
for(auto [a, b, c] : arr){
events[a].pb(c);
events[b+1].pb(-c);
}
vector<int> ans(n+1, 0);
for(int i = 0; i<=n; i++){
for(int x : events[i]){
if(x < 0) pres.erase(-x);
else pres.insert(x);
}
if(pres.size()) ans[i] = *pres.begin();
else ans[i] = 0;
}
return ans;
}
This gives an $$$O(n^2 \log n + q)$$$ solution as we need a set.
$$$O(n^2 \log n)$$$ can't seem to pass with $$$n \leq 7000$$$, so can we cut off the log?
Please read the hints above, most of the solution is contained in there.
Yes, we can cut the log, and there are many ways to do so. Here I will present one of them.
So for a fixed $$$l$$$, over many choices of $$$l'$$$ such that the interval of valid $$$len$$$ starts at some $$$lo$$$, we would want to pick the $$$l'$$$ that has the highest $$$hi$$$ of valid $$$len$$$. This is since greedily, a $$$l'$$$ with more candidates is better. Then we can sort these intervals in linear time with counting sort; we can sort by left endpoint by simply storing for each left endpoint the best right endpoint (and its $$$l'$$$) and just looping over the left endpoints in order from $$$1 \dots n$$$.
So after we have sorted these intervals, we can set $$$len \in [intervals_{i, left}, \min(intervals_{i, right}, intervals_{i+1, left}-1)]$$$ with the $$$l'$$$ associated with that interval. This will amortize as each $$$len$$$ is acted on at most once by some interval (or not acted on at all).
The final complexity is $$$O(n)$$$ processing for each $$$l$$$, giving a total of $$$O(n^2 + q)$$$.
The contestant yam had such a clean code, I just stole his instead of the model. :thumbs:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#define all(x) (x).begin(), (x).end()
const int N = 7007;
int n, q;
string s;
int p[N][N], ans[N][N];
int main() {
cin.tie(0)->sync_with_stdio(false);
cin >> n >> q >> s;
s = " " + s;
for (int i = n; i >= 1; i--)
for (int j = n; j >= 1; j--)
p[i][j] = (s[i] == s[j] ? p[i + 1][j + 1] + 1 : 0);
for (int i = 1; i <= n; i++) {
vector<array<int, 2>> pts(n + 1);
for (int j = 1; j <= n; j++) {
int l = i + p[i][j], r = j + p[i][j];
if (max(l, r) > n)
continue;
// range: l -> l + p[l + 1][r + 1]
pts[l] = max(pts[l], {l + p[l + 1][r + 1], j});
}
int r = -1;
for (int j = 1; j <= n; j++) {
for (int k = max(r + 1, j); k <= pts[j][0]; k++)
ans[i][k] = pts[j][1];
r = max(r, pts[j][0]);
}
}
while (q--) {
int l, r;
cin >> l >> r;
if (!ans[l][r])
cout << 0 << ' ' << 0 << '\n';
else {
cout << ans[l][r] << ' ' << ans[l][r] + (r - l) << '\n';
}
}
return 0;
}
Advanced G: Mayoi Tree
By the linearity of expectation, we can find the expected number of steps to go from node $$$u$$$ to node $$$v$$$ as the expected amount of time to cross each edge for the first time.
Solve the subtask for $$$t = 1$$$. How do you compute the expected number of steps needed go to from node $$$u$$$ to its parent?
Let $$$P_u(v)$$$ be the probability you go to node $$$v$$$ in $$$1$$$ step if you start at node $$$u$$$.
Let $$$E_u(v)$$$ denote the expected number of steps needed to go from node $$$u$$$ to node $$$v$$$ (note that $$$E_u(v)$$$ is not necessarily equal to $$$E_v(u)$$$).
Let $$$p_u$$$ denote the parent of node $$$u$$$ ($$$p_1$$$ is undefined).
Let $$$c_u$$$ denote the children of node $$$u$$$, or all the nodes adjacent to node $$$u$$$ other than $$$p_u$$$ (if it exists).
Let $$$up_u$$$ denote the expected number of steps needed to go from $$$u$$$ to $$$p_u$$$ (as before, $$$up_1$$$ is undefined). The most important observation is that we can define $$$up_u$$$ as a linear equation consisting of $$$up_u$$$, $$$up_v$$$ for $$$v \in c_u$$$ and $$$P_u(v)$$$ (with $$$up_u$$$ on both sides of the equation).
This is because there is a $$$P_u(p)$$$ chance to "escape" instantly and a $$$P_v(u)$$$ chance to go into the subtree of any $$$v$$$ which is a child of $$$u$$$. Most important, the expected amount of steps it takes is $$$1 + up_v + up_u$$$. You take $$$1$$$ step to go to node $$$v$$$, then you take $$$up_v$$$ steps to get back to node $$$u$$$, and finally, you take $$$up_u$$$ steps to "escape."
Let $$$down_u$$$ denote the expected number of steps needed to go from $$$p_u$$$ to $$$u$$$ (as before, $$$down_1$$$ is undefined). The same trick works for defining $$$down_u$$$.
Let $$$prob(u)$$$ denote the probability you go from node $$$p_u$$$ to node $$$u$$$. In particular, $$$prob(1) = 0$$$.
We can precompute $$$up_u$$$ with a bottom-up dfs and $$$down_u$$$ with a top-down dfs.
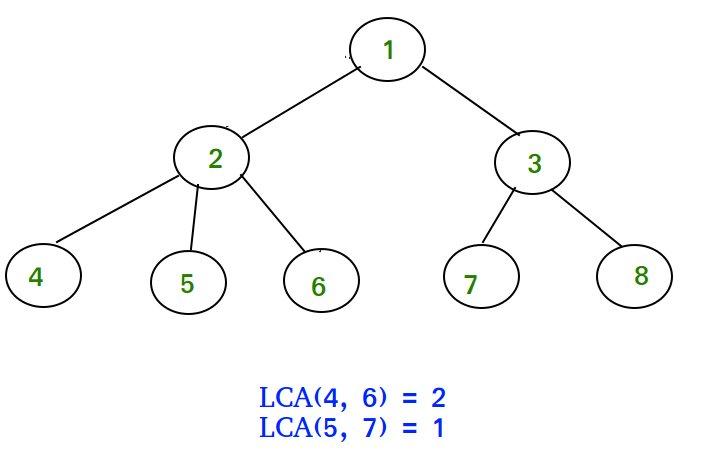
Finally, to answer a query of $$$s \ t$$$, let's first find the lca (least common ancestor) $$$l$$$ of $$$s$$$ and $$$t$$$. We then need to sum $$$up_u$$$ on the path from $$$s$$$ to $$$l$$$ (excluding $$$l$$$) and sum $$$down_u$$$ on the path from $$$l$$$ to $$$t$$$ (excluding $$$l$$$).
This can be done with prefix sums and any reasonable lca algorithm like binlifting or HLD. The final complexity is $$$O(n \log mod + n \log n)$$$.
#include <iostream>
#include <cmath>
#include <utility>
#include <cassert>
#include <algorithm>
#include <vector>
#include <array>
#include <functional>
#define sz(x) ((int)(x.size()))
#define all(x) x.begin(), x.end()
#define pb push_back
#ifndef LOCAL
#define cerr while(0) cerr
#endif
using ll = long long;
const ll mod = (1 << (23)) * 119 +1, ll_max = 1e18;
const int MX = 2e5 +10, int_max = 0x3f3f3f3f;
struct {
template<class T>
operator T() {
T x; std::cin >> x; return x;
}
} in;
using namespace std;
struct hld{
vector<int> dep, sz, par, head, tin, out, tour;
vector<vector<int>> adj;
int n, ind;
hld(){}
hld(vector<pair<int, int>> edges, int rt = 1){
n = sz(edges) + 1;
ind = 0;
dep = sz = par = head = tin = out = tour = vector<int>(n+1, 0);
adj = vector<vector<int>>(n+1);
for(auto [a, b] : edges){
adj[a].pb(b);
adj[b].pb(a);
}
dfs(rt, 0);
head[rt] = rt;
dfs2(rt, 0);
}
void dfs(int x, int p){
sz[x] = 1;
dep[x] = dep[p] + 1;
par[x] = p;
for(auto &i : adj[x]){
if(i == p) continue;
dfs(i, x);
sz[x] += sz[i];
if(adj[x][0] == p || sz[i] > sz[adj[x][0]]) swap(adj[x][0], i);
}
}
void dfs2(int x, int p){
tour[ind] = x;
tin[x] = ind++;
for(auto &i : adj[x]){
if(i == p) continue;
head[i] = (i == adj[x][0] ? head[x] : i);
dfs2(i, x);
}
out[x] = ind;
}
int k_up(int u, int k){
if(dep[u] <= k) return -1;
while(k > dep[u] - dep[head[u]]){
k -= dep[u] - dep[head[u]] + 1;
u = par[head[u]];
}
return tour[tin[u] - k];
}
int lca(int a, int b){
while(head[a] != head[b]){
if(dep[head[a]] > dep[head[b]]) swap(a, b);
b = par[head[b]];
}
if(dep[a] > dep[b]) swap(a, b);
return a;
}
} tr;
ll sum[MX], inv[MX], weight[MX]; //1/sum[u], weight to escape
vector<pair<int, ll>> adj[MX]; //node v and weight from u -> v
int par[MX], dep[MX];
ll up[MX], down[MX];
ll pup[MX], pdown[MX];
int n, q;
ll binpow(ll a, ll b = mod-2){
if(a == 0 && b == mod-2){
cout << "-1\n";
exit(1);
}
ll ans = 1;
for(int i = 1; i<=b; i*=2){
if(i&b) (ans *= a) %= mod;
(a *= a) %= mod;
}
return ans;
}
void dfs(int u, int p){
par[u] = p;
dep[u] = dep[p]+1;
sum[u] = 0;
for(auto [v, w] : adj[u]){
sum[u] += w;
if(v == p){
weight[u] = w;
}else{
dfs(v, u);
}
}
inv[u] = binpow(sum[u]);
}
//up[u] denotes the EV to start at node u and escape to the parent
//up[1] is undefined
//up[u] = sum(prob(of going to v)(up[v] + up[u] + 1)) + (prob of escaping now)
//up[u](1 + sum of probs) = sum of prob * (up[v] + 1) + prob of escaping now
//down[u] denotes the EV to start at the parent of node u and escape to node u
//down[1] is undefined
//down[u] = (prob of going up)(down[par[u]] (or 0 if u is the root) + down[u] + 1) + (prob of going to v when v != u)(up[v] + down[u] + 1) + (prob of going to u)
//(1 - prob of going up -prob of going to v for v != u from p)down[u] = prob of going up*(down[par[u]]+1) + prob of going to v * (up[v] + 1) + prob of going to u
void get_up(int u, int p){
ll go_down = 0, prob = 0;
for(auto [v, w] : adj[u]){
if(v == p) continue;
get_up(v, u);
ll pr = 1ll*w*inv[u]%mod;
go_down += pr*(up[v] + 1)%mod;
prob += pr;
}
go_down %= mod;
prob %= mod;
if(p != 0){
ll escape = weight[u]*inv[u]%mod;
up[u] = (go_down + escape)*binpow(1 + mod - prob)%mod;
}
}
void get_down(int u, int p){
//find it for all the children
ll go_down = 0;
ll go_up = (p == 0 ? 0 : (weight[u]*inv[u])%mod*(down[u] + 1)%mod);
ll prob = (p == 0 ? 0 : (weight[u]*inv[u]%mod));
for(auto [v, w] : adj[u]){
if(v == p) continue;
ll pr = 1ll*w*inv[u]%mod;
go_down += pr*(up[v]+1)%mod;
prob += pr;
}
go_down %= mod;
prob %= mod;
for(auto [v, w] : adj[u]){
if(v == p) continue;
ll pr = 1ll*w*inv[u]%mod;
go_down += mod - pr*(up[v]+1)%mod;
prob += mod - pr;
prob %= mod;
go_down %= mod;
down[v] = (go_up + go_down + pr)*binpow(1 + mod - prob)%mod;
prob += pr;
go_down += pr*(up[v]+1)%mod;
prob %= mod;
go_down %= mod;
get_down(v, u);
}
}
void get_psum(int u, int p){
for(auto [v, w] : adj[u]){
if(p == v) continue;
pup[v] = (pup[u] + up[v])%mod;
pdown[v] = (pdown[u] + down[v])%mod;
get_psum(v, u);
}
}
ll answer(int s, int t){
int l = tr.lca(s, t);
ll u = pup[s] + mod - pup[l];
ll d = pdown[t] + mod - pdown[l];
return (u + d)%mod;
}
void cl(){
for(int i = 1; i<=n; i++){
adj[i].clear();
par[i] = weight[i] = inv[i] = dep[i] = 0;
up[i] = down[i] = pup[i] = pdown[i] = 0;
}
}
void solve(){
n = in, q = in;
vector<pair<int, int>> edges;
for(int i = 2; i<=n; i++){
int u = in, v = in;
int a = in, b = in;
adj[u].pb({v, a});
adj[v].pb({u, b});
edges.push_back({u, v});
}
tr = hld(edges);
dfs(1, 0);
get_up(1, 0);
get_down(1, 0);
get_psum(1, 0);
for(int i = 1; i<=q; i++){
int s = in, t = in;
cout << answer(s, t) << "\n";
}
cl();
}
signed main(){
cin.tie(0) -> sync_with_stdio(0);
int T = 1;
cin >> T;
for(int i = 1; i<=T; i++){
solve();
}
return 0;
}
Advanced I: Fire Fighters
You can know the winner of a prefix with simulation.
You can know the winner of a suffix with dp and an stack.
Think about the parity of the length of the subarray $$$[l, r]$$$.
The hints briefly sum up the solution of the problem step by step, but we will provide a more detailed explanation now.
Each query splits the array into three parts, the subarray $$$[0, l-1]$$$, the subarray $$$[l, r]$$$, and the subarray $$$[r + 1, n]$$$.
First, we need to calculate the winner of each prefix with a simple simulation, let the winner of the $$$i$$$-th prefix be $$$pre_{i}$$$.
We also have to calculate the winner of each suffix with dp and an stack to find the closest element greater or equal to the right.
To know what happens in the suffix $$$[l, n-1]$$$ we have to think about three cases:
If $$$a_{pre_{i}}$$$ is greater than every element in the suffix $$$[l, n-1]$$$ the winner of the tournament will be $$$pre_{i}$$$.
If value $$$x$$$ of the query is greater or equal to $$$a_{pre_{i}}$$$ we have to check the parity of the length subarray and if it's even the answer will be the winner of the suffix $$$[r+1, n-1]$$$.
Otherwise, if the length of the subarray is odd, the winner will be either $$$r$$$, or the winner of the subarray $$$[r+1, n-1]$$$. This can be checked in the same way as the first case and if x is not greater than every element in the subarray $$$[r+1, n-1]$$$ it can be shown the answer will be the winner of the suffix $$$[r+1, n-1]$$$.
Time Complexity: $$$O(n)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
const int N = 69e4 + 4, inf = INT_MAX;
int t, n, q, a[N], nxt[N], dp[N], pre[N];
pair<int, int> sufMx[N];
stack<int> st;
int solve(int idx, int x, int r) {
if (x > sufMx[r].first) return idx;
else if (x == sufMx[r].first) return dp[sufMx[r].second+1];
else return dp[r];
}
signed main() {
ios::sync_with_stdio(false); cin.tie(nullptr);
cin >> t;
while (t--) {
cin >> n >> q;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
st = stack<int>();
for (int i = n-1; i >= 0; i--) {
while (!st.empty() && a[st.top()] < a[i]) st.pop();
int x = (st.empty() ? n : st.top());
if (st.empty()) {
dp[i] = i;
nxt[i] = n;
}
else if (a[x] == a[i]) {
dp[i] = (x+1 < n ? dp[x+1] : n);
nxt[i] = x+1;
}
else {
dp[i] = dp[x];
nxt[i] = x;
}
st.push(i);
}
nxt[n] = dp[n] = pre[n] = n;
int x = 0;
for (int i = 0; i < n; i++) {
if (nxt[x] == i) x = nxt[x];
pre[i] = x;
}
sufMx[n] = make_pair(-inf, n);
for (int i = n-1; i >= 0; i--) {
if (a[i] > sufMx[i+1].first) sufMx[i] = make_pair(a[i], i);
else sufMx[i] = sufMx[i+1];
}
while (q--) {
int l, r, x;
cin >> l >> r >> x;
l--; r--;
int y = (l ? pre[l-1] : -1);
if (y == -1 || a[y] < x) {
if (!((r-l+1) & 1)) cout << dp[r+1]+1 << "\n";
else {
cout << solve(r, x, r+1)+1 << "\n";
}
}
else if (a[y] == x) {
if (!((r-l+2) & 1)) cout << dp[r+1]+1 << "\n";
else {
cout << solve(r, x, r+1)+1 << "\n";
}
}
else { // a[y] > x
cout << solve(y, a[y], r+1)+1 << "\n";
}
}
}
}
Advanced J: Arknights Chips
Solve the problem in $$$O(n)$$$ or $$$O(n \log n)$$$.
Let $$$p = \frac{a}{100}$$$ and $$$q = 1 - p$$$.
The answer is
$$$i$$$ enumerates the number of sniper chips obtained.
$$$\lfloor{\frac{a}{b}}\rfloor = \frac{a}{b} - \frac{a \text{ mod } b}{b}$$$
How can we frame the question in terms of $$${n - i} \text{ mod } {x}$$$?
For simplicity, let's have $$$i$$$ enumerate the number of caster chips instead of the sniper chips.
Then using the definition of floor, we can rewrite this as
$$$\sum_{i = 0}^{n} {n \choose i}p^{i}q^{n - i} i = pn$$$ (this can be interpreted as "If you have a coin that flips heads with probability $$$p$$$ and tails with probability $$$1 - p$$$, what is the expected number of heads you obtain after $$$n$$$ flips?")
So now the question boils down to finding the expected value of $$$ \text{# caster chips mod } x$$$.
Let $$$f_m(n)$$$ denote the probability that after $$$n$$$ clears, the number of caster chips is $$$m \text{ mod } x$$$. We can observe that $$$f_0(0) = 1$$$ and $$$f_m(n) = p f_{m}(n-1) + q f_{(m + x - 1) \text { mod }}^(n-1)$$$. With probability $$$p$$$, we can get a sniper chip from a state where $$$\text{# caster chips} \equiv m \pmod{x}$$$ and with probability $$$q$$$, we can get a caster chip from a state where $$$\text{# caster chips} \equiv m - 1 \pmod{x}$$$. Additionally, with $$$0$$$ stage clears, there is a probability of $$$1$$$ that the number of caster chips is $$$0 \text {mod } x$$$ (as it is $$$0$$$).
This motivates matrix exponentiation as the method to compute $$$f_m(n)$$$, as the sum we desire is $$$\sum_{i = 0}^{x-1} if_{i}(n)$$$. We can make a matrix $$$A$$$ where on row $$$i$$$, $$$A_{i}{i} = p$$$ and $$$a_{i}{(i + 1) \text{ mod } x} = q$$$ and all other cells are $$$0$$$. By raising this to the power of $$$n$$$, we can find $$$f_m(n)$$$ as $$$A_{0}{m}$$$.
The final sum is
The total complexity is $$$O(x^3 \log n)$$$ with binary exponentiation for the matrix.
#include <iostream>
#include <cmath>
#include <utility>
#include <cassert>
#include <algorithm>
#include <vector>
#include <array>
#define sz(x) ((int)(x.size()))
#define all(x) x.begin(), x.end()
#define pb push_back
using ll = long long;
const ll mod = (1 << (23)) * 119 +1;
using namespace std;
ll binpow(ll a, ll b = mod-2){
a %= mod;
ll ans = 1;
for(ll i = 1; i<=b; i*=2ll){
if(i&b){
(ans *= a) %= mod;
}
(a *= a) %= mod;
}
return ans;
}
#define matrix vector<vector<ll>>
matrix mult(matrix& a, matrix& b){
matrix c = a;
for(auto& x : c){
fill(all(x), 0);
}
for(int i = 0; i<sz(a); i++){
for(int j = 0; j<sz(a); j++){
if(a[i][j] == 0) continue;
for(int k = 0; k<sz(a); k++){
c[i][k] += a[i][j]*b[j][k]%mod;
}
}
}
for(int i = 0; i<sz(c); i++){
for(int j = 0; j<sz(c); j++){
c[i][j] %= mod;
}
}
return c;
}
matrix binpow(matrix a, ll b){
matrix ans = a;
for(int i = 0; i<sz(ans); i++){
fill(all(ans[i]), 0);
ans[i][i] = 1;
}
for(ll i = 1; i<=b; i*=2){
if(i&b){
ans = mult(ans, a);
}
a = mult(a, a);
}
return ans;
}
void solve(){
int a;
ll x, y, n;
cin >> a >> x >> y >> n;
ll inv = binpow(x);
ll p = a*binpow(100)%mod;
ll q = 1 + mod - p;
ll ans = p*(n%mod)%mod + inv*y%mod*q%mod*(n%mod);
ans %= mod;
matrix base(x, vector<ll>(x, 0));
for(int i = 0; i<x; i++){
base[i][i] = p;
base[i][(i + 1)%x] = q;
}
auto mat = binpow(base, n);
for(int i = 0; i<x; i++){
ans += (mod - inv)*y%mod*i%mod*mat[0][i]%mod;
ans %= mod;
}
cout << ans << "\n";
}
signed main(){
cin.tie(0) -> sync_with_stdio(0);
int T = 1;
cin >> T;
for(int i = 1; i<=T; i++){
solve();
}
return 0;
}
Solve in $$$O(x^2 \log n)$$$
Each row is a cyclic shift of the row above it, so instead of storing the entire matrix, we only have to store the first row. This also means we only have to multiply two vectors together instead of two matrices, giving an $$$O(x^2 \log n)$$$ solution.
Solve in $$$O(x \log x \log n)$$$
We only realized this solution existed after the contest was over.
You can submit at problem G in this mashup.
We can see $$$f_m(n)$$$ as $$$[z^m](p + qz)^n \text{ mod } (z^x -1)$$$. We can exponentiate the polynomial in $$$O(x \log x \log n)$$$ time with binary exponential. By using NTT to multiply polynomials, we will never need more than $$$2x$$$ intermediary terms.
Advanced K: ANDtreew
Think about Kruskal Reconstruction Tree.
We will use the common technique in bitwise problems of adding the bits one by one from most to least significant.
We want to check if we can add a bit to the answer in $$$O(k)$$$, to do so we can precompute so values which will help us determine if the children of a node that are not in the query (i.e those that can't be removed), have the value of the AND we want as a submask.
You can do this "naively" with an AND sparse table for each adjacency list.
Alternatively, we can just count the number of children that have each bit for every node, and then for each query precompute the maximal set of bits that the AND can have for that node to be good.
The hints briefly sum up the solution of the problem step by step, but we will provide a more detailed explanation now.
For the minimum value of a tree to change, so that the value of the whole forest can increment, it is needed that the minimum node is removed. With this in mind, we can build another tree recursively in the following way (we will call it $$$G$$$ for clarity):
- Given a tree, if the tree consists of a single node, we stop there.
- If there it consists of at least $$$2$$$ nodes, we take the node with the minimum value and and remove it from the tree, decomposing it into several other trees. We take the minimum nodes of those trees and add them as children in $$$G$$$ to the node we removed from the original tree. Then, do the same for the decomposed trees.
$$$G$$$ is also known as the Kruskal Reconstruction Tree, so we will refer to it as Kruskal Tree from now on.
Once we've build the Kruskal tree, we will iterate for each query over the bits of the answer from most significant bit to less significant bit, and try to add those to the AND as we progress. For a specific desired value of AND $$$mask$$$, we will define each node $$$v$$$ as good if and only if $$$mask$$$ is a submask of its value (i.e. $$$v \ AND \ mask = mask$$$) or it can be removed (i.e. there's some $$$i$$$ such that $$$x_i = v$$$) and all of its children are good. If we manage to quickly compute if the root of the Kruskal Tree is good, we can know whether it is possible to have $$$mask$$$ as a submask of the answer or not.
There are multiple ways to do this in $$$O(k)$$$, resuling in a total complexity of $$$O(k \log n)$$$ per query. I will present two.
The first one, which was the original intended solution proposed by the author, is to build an AND sparse table for each adjacency list. Therefore, for each value of $$$mask$$$, one can do a DFS and, for each node, check if it is good. Firstly, we check if it has $$$mask$$$ as a submask, because if it does it is already good. If it doesn't, we will proceed with the DFS with the children that are in the query, and check if those are good, if any of those is not good, then the node will already not be good. Additionally, to check that the children which are not in the query (and therefore cannot be removed) have $$$mask$$$ as a submask, we will query for each interval between the indices of the children in the query the AND of those children, to get the AND of all the children that are not in the query. All that is left to check is that $$$mask$$$ is a submask of the AND the children for the node to be good.
The second way to check if a node is good fast is to precalculate for each node the count of the ocurrences of each bit in its children. Then, in a query, you can precalculate before checking if any $$$mask$$$ is good a "bad mask", which will contain all of the bits that $$$mask$$$ cannot have for that node to be good. In other words, we will store for which bits there exists a children of the node which cannot be removed and does not have that bit on. To do so, we go over every node in the query and, for each node, we iteare over all the bits. For each bit, we will iterate over all the children that are in the query and, if they do not have that bit on add it to the count of children with the bit on (because, as we only want to know if the children which can't be removed have the bit on, this does not affect us and makes the implementation easier). Therefore, each bit will not be bad if and only if its count is equal to the number of children (both in and not in the query) of the node, because all the children that are in the query will have added to the count, therefore if it is not equal to the number of children one child which is not in the query must not have it.
#include <bits/stdc++.h>
using namespace std;
const int LOG = 20;
struct DSU{
vector<int> v, mn;
void init(int n){
v.assign(n, -1);
mn.resize(n);
for(int i = 0; i < n; i++) mn[i] = i;
}
int get(int x){return v[x] < 0 ? x : v[x] = get(v[x]);}
void unite(int x, int y){
x = get(x); y = get(y);
if(x == y) return;
if(v[x] > v[y]) swap(x, y);
v[x] += v[y]; v[y] = x;
mn[x] = min(mn[x], mn[y]);
}
int getMn(int i){
return mn[get(i)];
}
};
void buildSparse(vector<int>& v, vector<vector<int>>& sparse){
int n = (int)v.size();
sparse.assign(LOG, vector<int>(n));
for(int k = 0; k < LOG; k++){
for(int i = 0; i < n; i++){
if(k == 0) sparse[k][i] = v[i]+1;
else{
if(i - (1 << (k-1)) < 0) sparse[k][i] = sparse[k-1][i];
else sparse[k][i] = (sparse[k-1][i] & sparse[k-1][i - (1 << (k-1))]);
}
}
}
}
int getAnd(int l, int r, vector<vector<int>>& sparse){
if(l > r) return (1 << LOG) - 1;
int k = 31 - __builtin_clz(r-l+1);
return (sparse[k][r] & sparse[k][l + (1 << k) - 1]);
}
int taken;
bool DFS(int x, vector<vector<int>>& adj, vector<vector<int>>& specialAdj, vector<vector<vector<int>>>& sparses, int curr){
if(((x+1) & curr) == curr) {taken++; return true;}
//It needs to be removed;
int lst = -1;
int ans = (1 << LOG) - 1;
for(int ind : specialAdj[x]){
if(!DFS(adj[x][ind], adj, specialAdj, sparses, curr)) return false;
ans &= getAnd(lst + 1, ind-1, sparses[x]);
lst = ind;
}
ans &= getAnd(lst + 1, (int)adj[x].size() - 1, sparses[x]);
if((ans & curr) == curr) return true;
else return false;
}
void undo(vector<int>& x, vector<int>& parent, vector<vector<int>>& specialAdj){
for(int i : x){
if(parent[i] != -1) specialAdj[parent[i]].pop_back();
}
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
int tt; cin >> tt;
while(tt--){
int n, q; cin >> n >> q;
vector<vector<int>> originalAdj(n);
for(int i = 0; i < n - 1; i++){
int u, v; cin >> u >> v; u--; v--;
originalAdj[u].push_back(v);
originalAdj[v].push_back(u);
}
vector<vector<int>> adj(n);
vector<int> ind(n, -1), parent(n, -1);
DSU UF; UF.init(n);
for(int i = n - 1; i >= 0; i--){
for(int node : originalAdj[i]){
if(node < i) continue;
adj[i].push_back(UF.getMn(node));
UF.unite(i, node);
}
sort(adj[i].begin(), adj[i].end());
for(int j = 0; j < (int)adj[i].size(); j++){
ind[adj[i][j]] = j;
parent[adj[i][j]] = i;
}
}
vector<vector<vector<int>>> sparses(n);
for(int i = 0; i < n; i++){
buildSparse(adj[i], sparses[i]);
}
vector<vector<int>> specialAdj(n);
while(q--){
int k; cin >> k;
vector<int> x(k);
bool zero = false;
for(int i = 0; i < k; i++){
cin >> x[i]; x[i]--;
if(!x[i]) zero = true;
if(parent[x[i]] != -1){
specialAdj[parent[x[i]]].push_back(ind[x[i]]);
}
}
if(!zero){
cout << 1 << "\n";
undo(x, parent, specialAdj);
continue;
}
int ans = 0;
int curr = 0;
for(int b = LOG - 1; b >= 0; b--){
curr += (1 << b);
taken = 0;
if(DFS(0, adj, specialAdj, sparses, curr) && (taken > 0 || k != n)) ans = curr;
else curr -= (1 << b);
}
cout << ans << "\n";
undo(x, parent, specialAdj);
}
}
}
#include <bits/stdc++.h>
using namespace std;
const int LOG = 20;
struct DSU{
vector<int> v, mn;
void init(int n){
v.assign(n, -1);
mn.resize(n);
for(int i = 0; i < n; i++) mn[i] = i;
}
int get(int x){return v[x] < 0 ? x : v[x] = get(v[x]);}
void unite(int x, int y){
x = get(x); y = get(y);
if(x == y) return;
if(v[x] > v[y]) swap(x, y);
v[x] += v[y]; v[y] = x;
mn[x] = min(mn[x], mn[y]);
}
int getMn(int i){
return mn[get(i)];
}
};
int taken;
bool DFS(int x, vector<vector<int>>& specialAdj, vector<int>& badMask, int curr){
if(((x+1) & curr) == curr) {taken++; return true;}
if(badMask[x] & curr) return false;
//It needs to be removed;
for(int node : specialAdj[x]){
if(!DFS(node, specialAdj, badMask, curr)) return false;
}
return true;
}
void setBad(int x, vector<vector<int>>& adj, vector<vector<int>>& specialAdj, vector<vector<int>>& cnt, vector<int>& badMask){
for(int k = 0; k < LOG; k++){
int hvTotal = cnt[k][x];
for(int node : specialAdj[x]){
if(!((1 << k) & (node+1))) hvTotal++;
}
if(hvTotal != (int)adj[x].size()) badMask[x] += (1 << k);
}
for(int node : specialAdj[x]){
setBad(node, adj, specialAdj, cnt, badMask);
}
}
void undo(vector<int>& x, vector<int>& parent, vector<vector<int>>& specialAdj, vector<int>& badMask){
for(int i : x){
badMask[i] = 0;
if(parent[i] != -1) specialAdj[parent[i]].pop_back();
}
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
int tt; cin >> tt;
while(tt--){
int n, q; cin >> n >> q;
vector<vector<int>> originalAdj(n);
for(int i = 0; i < n - 1; i++){
int u, v; cin >> u >> v; u--; v--;
originalAdj[u].push_back(v);
originalAdj[v].push_back(u);
}
vector<vector<int>> adj(n);
vector<int> parent(n, -1);
DSU UF; UF.init(n);
for(int i = n - 1; i >= 0; i--){
for(int node : originalAdj[i]){
if(node < i) continue;
adj[i].push_back(UF.getMn(node));
UF.unite(i, node);
}
sort(adj[i].begin(), adj[i].end());
for(int j = 0; j < (int)adj[i].size(); j++){
parent[adj[i][j]] = i;
}
}
vector<vector<int>> cnt(LOG, vector<int>(n, 0));
for(int k = 0; k < LOG; k++){
for(int i = 0; i < n; i++){
for(int node : adj[i]){
if((1 << k) & (node+1)) cnt[k][i]++;
}
}
}
vector<vector<int>> specialAdj(n);
vector<int> badMask(n, 0);
while(q--){
int k; cin >> k;
vector<int> x(k);
bool zero = false;
for(int i = 0; i < k; i++){
cin >> x[i]; x[i]--;
if(!x[i]) zero = true;
if(parent[x[i]] != -1){
specialAdj[parent[x[i]]].push_back(x[i]);
}
}
if(!zero){
cout << 1 << "\n";
undo(x, parent, specialAdj, badMask);
continue;
}
setBad(0, adj, specialAdj, cnt, badMask);
int ans = 0;
int curr = 0;
for(int b = LOG - 1; b >= 0; b--){
curr += (1 << b);
taken = 0;
if(DFS(0, specialAdj, badMask, curr) && (taken > 0 || k != n)) ans = curr;
else curr -= (1 << b);
}
cout << ans << "\n";
undo(x, parent, specialAdj, badMask);
}
}
}
Advanced L: Everyone Loves Threes Magic (Hard)
Solve in $$$O(R - L)$$$.
Let $$$f(i)$$$ be $$$0$$$ if $$$i$$$ is not divisible by $$$3$$$ or the number of $$$3$$$'s in the base-$$$10$$$ representation of $$$i$$$ otherwise.
Unfortunately, we cannot evaluate this in $$$O(R - L)$$$ as $$$R$$$ is very large.
We can reduce the problem to finding $$$\sum_{i = 1}^{x-1} f(i)$$$, $$$\sum_{i = 1}^{x-1} if(i)$$$, and $$$\sum_{i = 1}^{x-1} i^2f(i)$$$ for a very large $$$x$$$.
Let $$$d(x)$$$ denote the sum of digits in the base-$$$10$$$ representation $$$\text{ mod } 3$$$. For instance $$$d(1) = 1, d(55) = 1, d(3366) = 0$$$.
Let $$$val(i, j) = \sum\limits_{d(x) = j, \log_{10}(x) < i} x^0$$$.
Let $$$lin(i, j) = \sum\limits_{d(x) = j, \log_{10}(x) < i} x^1$$$.
Let $$$squ(i, j) = \sum\limits_{d(x) = j, \log_{10}(x) < i} x^2$$$.
Let $$$sum(i, j) = \sum\limits_{d(x) = j, \log_{10}(x) < i} x^0f(x)$$$.
Let $$$slin(i, j) = \sum\limits_{d(x) = j, \log_{10}(x) < i} x^1f(x)$$$.
Let $$$ssqu(i, j) = \sum\limits_{d(x) = j, \log_{10}(x) < i} x^2f(x)$$$.
I would give math formulas for all of these, but its easier to just attach code.
void precomp(int n){
ll p = 1;
for(int i = 0; i<=n; i++){
ip10[i] = p;
(p *= 10ll) %= mod;
}
p = 1;
val[0][0] = 1;
for(int i = 0; i<=n; i++){
for(int j = 0; j<3; j++){
for(int k = 0; k<10; k++){
ll d = p*k%mod;
if(k == 3){
//(cnt(i) + 1)
//1
(sum[i+1][(j+k)%3] += val[i][j]) %= mod;
//(i + d)(cnt(i) + 1)
//i
//d
(slin[i+1][(j+k)%3] += val[i][j]*d%mod + lin[i][j]) %= mod;
//(i + d)(i + d)(cnt(i) + 1)
//i^2
//id
//di
//d^2
(ssqu[i+1][(j+k)%3] += val[i][j]*d%mod*d%mod + 2ll*lin[i][j]*d%mod + squ[i][j]) %= mod;
}
//(cnt(i))
//cnt(i)
(sum[i+1][(j+k)%3] += sum[i][j]) %= mod;
//(i + d)(cnt(i))
//icnt(i)
//dcnt(i)
(slin[i+1][(j+k)%3] += sum[i][j]*d%mod + slin[i][j]) %= mod;
//(i + d)(i + d)(cnt(i))
//i^2 cnt[i]
//idcnt(i)
//dicnt(i)
//d^2cnt(i)
(ssqu[i+1][(j+k)%3] += sum[i][j]*d%mod*d%mod + 2ll*slin[i][j]*d%mod + ssqu[i][j]) %= mod;
(val[i+1][(j+k)%3] += val[i][j]) %= mod;
(lin[i+1][(j+k)%3] += val[i][j]*d%mod + lin[i][j]) %= mod;
(squ[i+1][(j+k)%3] += val[i][j]*d%mod*d%mod + 2ll*lin[i][j]*d%mod + squ[i][j]) %= mod;
}
}
(p *= 10) %= mod;
}
}
Let's fix some numbers $$$y$$$ and $$$k$$$ such that $$$y + 10^k \leq x$$$. We can easily obtain the sum of $$$f(i)$$$, $$$if(i)$$$, and $$$i^2f(i)$$$ for this range $$$[y, y+10^k)$$$ with the precomputed six precomputed functions above as we have no restrictions on the digits; The sum of $$$f(i)$$$, $$$if(i)$$$, and $$$i^2f(i)$$$ within this range depends solely on $$$y$$$, $$$d(y)$$$, $$$k$$$, and the precomputed functions above.
Let $$$n$$$ denote the number of digits in $$$x$$$.
To use this fact efficiently, let's enumerate the number of digits $$$y$$$ has in common with $$$x$$$. If at the $$$k$$$'th digit from the left, the digit in $$$y$$$ is strictly less than the digit $$$x$$$ (it cannot be strictly more, and if they are the same, $$$k$$$ will increase). We can set the last $$$n - k$$$ of $$$y$$$ to be $$$0$$$ and evaluate the sum for $$$[y, y + 10^{n - k})$$$.
This way, every number $$$ < x$$$ will be accounted for.
This takes $$$O(\log_{10}(R))$$$ precompute and $$$O(\log_{10}(R))$$$ per testcase. Read the code for more impl details. Note that a traditional digit dp where you store a flag of whether or not the current digit is strictly less than $$$x$$$ or not also works, but it runs slower.
//misaka, hitori, and elaina will carry me to red
#pragma GCC optimize("O3,unroll-loops")
#pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
#include <iostream>
#include <cmath>
#include <utility>
#include <cassert>
#include <algorithm>
#include <vector>
#include <array>
#include <cstdio>
#include <cstring>
#include <functional>
#include <numeric>
#include <set>
#include <queue>
#include <map>
#include <chrono>
#include <random>
#define sz(x) ((int)(x.size()))
#define all(x) x.begin(), x.end()
#define pb push_back
#define eb emplace_back
#define kill(x, s) {if(x){ cout << s << "\n"; return ; }}
//#ifndef LOCAL
#define cerr while(0) cerr
//#endif
using ll = long long;
using lb = long double;
const lb eps = 1e-9;
//const ll mod = 1e9 + 7, ll_max = 1e18;
const ll mod = (1 << (23)) * 119 +1, ll_max = 1e18;
const int MX = 2e5 +10, int_max = 0x3f3f3f3f;
struct {
template<class T>
operator T() {
T x; std::cin >> x; return x;
}
} in;
using namespace std;
//(r - i+1)(i - l+1)sum[i]
//(r+1)(-l+1)sum[i] + (-(-l+1) + r+1)*i*sum[i] + -i^2*sum[i]
ll val[MX][3]; //the number of ways to pick i digits such that they sum to j mod 3
ll sum[MX][3]; //the number of 3's across all those ways
ll lin[MX][3]; //sum of dig for all x that satisfy (i, j)
ll squ[MX][3]; //sum of dig*dig for all x that satisify (i, j)
ll slin[MX][3]; //sum of sum*dig for all x
ll ssqu[MX][3]; //sum of sum*dig*dig for all x
ll ip10[MX]; //ipman orz!
void precomp(int n){
ll p = 1;
for(int i = 0; i<=n; i++){
ip10[i] = p;
(p *= 10ll) %= mod;
}
p = 1;
val[0][0] = 1;
for(int i = 0; i<=n; i++){
for(int j = 0; j<3; j++){
for(int k = 0; k<10; k++){
ll d = p*k%mod;
if(k == 3){
//(cnt(i) + 1)
//1
(sum[i+1][(j+k)%3] += val[i][j]) %= mod;
//(i + d)(cnt(i) + 1)
//i
//d
(slin[i+1][(j+k)%3] += val[i][j]*d%mod + lin[i][j]) %= mod;
//(i + d)(i + d)(cnt(i) + 1)
//i^2
//id
//di
//d^2
(ssqu[i+1][(j+k)%3] += val[i][j]*d%mod*d%mod + 2ll*lin[i][j]*d%mod + squ[i][j]) %= mod;
}
//(cnt(i))
//cnt(i)
(sum[i+1][(j+k)%3] += sum[i][j]) %= mod;
//(i + d)(cnt(i))
//icnt(i)
//dcnt(i)
(slin[i+1][(j+k)%3] += sum[i][j]*d%mod + slin[i][j]) %= mod;
//(i + d)(i + d)(cnt(i))
//i^2 cnt[i]
//idcnt(i)
//dicnt(i)
//d^2cnt(i)
(ssqu[i+1][(j+k)%3] += sum[i][j]*d%mod*d%mod + 2ll*slin[i][j]*d%mod + ssqu[i][j]) %= mod;
(val[i+1][(j+k)%3] += val[i][j]) %= mod;
(lin[i+1][(j+k)%3] += val[i][j]*d%mod + lin[i][j]) %= mod;
(squ[i+1][(j+k)%3] += val[i][j]*d%mod*d%mod + 2ll*lin[i][j]*d%mod + squ[i][j]) %= mod;
}
}
(p *= 10) %= mod;
}
}
#define info array<ll, 3>
//sum, slin, ssqu
info operator + (info a, info b){
return info{(a[0]+b[0])%mod, (a[1]+b[1])%mod, (a[2]+b[2])%mod};
}
info comb(int c, ll d, info a, info b){
//a is sum/slin/ssqu
//b is val/lin/squ
info r = {0ll, 0ll, 0ll};
r[0] = (a[0]+c*b[0]%mod)%mod;
r[1] = (a[1] + 1ll*c*b[1] + 1ll*d*a[0]%mod + 1ll*b[0]*d%mod*c%mod)%mod;
r[2] = (1ll*c*(b[2] + 2ll*d*b[1]%mod + d*d%mod*b[0]%mod)%mod + a[2] + 2ll*d*a[1]%mod + d*d%mod*a[0]%mod)%mod;
return r;
}
void pr(info& a){
for(auto x : a) cerr << x << " "; cerr << "\n";
}
info eval(string s){
ll d = 0;
int c = 0;
int m3 = 0;
info ret = {0ll, 0ll, 0ll};
cerr << "eval " << s << "\n";
for(int i = sz(s); i>=1; i--){
cerr << d << " " << c << " " << m3 << "\n";
for(int j = 0; j<s[sz(s)-i]-'0'; j++){
int nc = c + (j == 3);
ll nd = d + 1ll*j*ip10[i-1]%mod;
int nm3 = (m3 + j)%3;
cerr << i << " " << (char)(j + '0') << "\n";
info a = {sum[i-1][(3 - nm3)%3], slin[i-1][(3 - nm3)%3], ssqu[i-1][(3 - nm3)%3]};
info b = {val[i-1][(3 - nm3)%3], lin[i-1][(3 - nm3)%3], squ[i-1][(3 - nm3)%3]};
pr(a); pr(b);
auto tmp = comb(nc, nd, a, b);
pr(tmp);
ret = ret + tmp;
}
if(s[sz(s)-i] == '3') c++;
(m3 += (s[sz(s)-i] - '0')) %= 3;
(d += 1ll*(s[sz(s)-i] - '0')*ip10[i-1]) %= mod;
cerr << "\n";
}
return ret;
}
ll conv(string s){
ll ans = 0;
for(int i = sz(s)-1; i>=0; i--){
cerr << s[sz(s) - i-1] << " " << i << "\n";
ans += 1ll*(s[sz(s) - i-1]-'0')*ip10[i]%mod;
} cerr << "\n";
return ans%mod;
}
string add(string l){
for(int i = sz(l)-1; i>=0; i--){
if(l[i] == '9'){
l[i] = '0';
}else{
l[i]++;
break ;
}
}
if(l == string(l.size(), '0')){
l.pb('1');
reverse(all(l));
}
return l;
}
ll binpow(ll a, ll b = mod - 2){
ll ans = 1;
for(ll i = 1; i<=b; i*=2ll){
if(i&b) (ans *= a) %= mod;
(a *= a) %= mod;
}
return ans;
}
void solve(){
string l = (string) in;
string r = (string) in;
auto sl = eval(l);
auto sr = eval(add(r));
ll L = conv(l), R = conv(r);
//(r+1)(-l+1)sum[i] + (-(-l+1) + r+1)*i*sum[i] + -i^2*sum[i]
pr(sl);
pr(sr);
ll ans = 1ll*(R + 1)*(mod-L+1)%mod*(sr[0] + mod - sl[0])%mod + \
1ll*(L + mod - 1 + R + 1)*(sr[1] + mod - sl[1])%mod + \
1ll*(mod - 1)*(sr[2] + mod - sl[2])%mod;
ans %= mod;
ll len = (R + mod - L + 1)%mod;
cerr << ans << "\n";
cerr << L << " " << R << " " << len << "\n";
cout << ans%mod << "\n";
}
signed main(){
cin.tie(0) -> sync_with_stdio(0);
precomp(100010);
int T = 1;
cin >> T;
for(int i = 1; i<=T; i++){
//cout << "Case #" << i << ": ";
solve();
}
return 0;
}