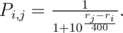Hi Codeforces.

I am glad to share a small but useful update of Polygon, which was fully developed by me in the walls of ITMO. Now preparing problems with unusual I/O will become a little easier.

Now in the new problems you will get examples in the statements without any transformations by LaTeX/HTML. If earlier you had difficulties with the correct formatting of empty lines or the fact that a double hyphen is replaced with a dash, now there are no such difficulties. The enhancement works for both PDF and HTML statements.

For example, to have such I/O examples just add such a test and use the appropriate output from the model solution.

Note that the feature to overwrite the examples is stayed working (custom content of input or output data for statements). It seems that there are almost no reasons to use it for an input now (apparently, only for interactive problems).

Previously created problems use the old approach, so this innovation should not break existing problems.

How do you like the feature?

Hi,

I am happy to announce that Lyft Level 5 Challenge 2018 — Final Round will be held in Palo Alto on Nov/04/2018 21:10 (Moscow time). The official round contains six problems and will last for two hours.

Winners will receive:

• First place: $2000
• Second place: $1000
• Third place: $500

Here is the list of onsite finalists:

If you are interested in an internship or a job at Lyft, follow the link below.

If you are not participating in the Final Round, you will be able to take part in rated open divisions. Each of them contains six problems and will last for two and a half hours.

This round was prepared by _h_, Lewin, majk, Noam527, stanislav.bezkorovainyi, and me.

Thank you to 300iq, cdkrot, BigBag, danya.smelskiy, Fekete, MrDindows, Nazikk, Sonechko, winger, MaxZubec for help with testing.

Special thanks to KAN for helping me with coordinating, MikeMirzayanov for Polygon and Codeforces, and Lyft for organizing this competition.

If you have never solved interactive problems before, please read this.

Scoring distribution:

Div1 and onsite:

750-1250-1500-2000-2750-3000

Div2:

500-1000-1750-2250-2500-3000

We have onsite issues, the contest was postponed by at least 5 minutes.

Because of the onsite round, the system testing will be in an hour after the round.

Contest is over!

Congratulations to the winners!

Onsite competition:

Div 1:

Div 2:

Editorial is available here.

Are you looking for photos from the onsite round? It is here.

Hi Codeforces!

Meet a small innovation on Codeforces — difficulties of problems (and at the same time a new widget filtering problems in the archive). For all the problems of the archive, I’ve calculated the difficulties in the scale of the rating of participants. Approximately this means that if the rating of the problem is equal to yours, then on a typical round you would solve the problem with a probability of 0.5. And, in general, if your rating is r_i, and the problem rating is r_j, then the problem during the round can be solved approximately with probability:

For example, if the rating of a problem is less than yours by 200, then the expected probability of solving the problem is 0.75. With a difference of 400 rating points, the probability increases to 0.9.

For convenient search of problems in the archive, you can now use a special widget:

With it, you can find not only problems that have all the chosen tags, but also which have at least one tag from the list.

A difficulty of a problem is also displayed when choosing problems in a mashup.

I hope that now you will be able to do more effective practice, and the process of making new mashups for trainings will become easier.

UPD 1: Have you already noticed new pop-ups about judgment verdicts of your submissions?

UPD 2: (API update) Optional field rating has been added to the object Problem in API.

UPDATE: The form for team registration appeared. Data will be transfered to ICPC database. Teams who filled similar form for the fixed site, do not need to fill this form twice..

Teams Registration

Coordinators of sites, allowing only teams from host university already received the links to similar forms with the pre-selected site.

The 2018 ICPC Uzbekistan Subregional Contest will take place in multi-host mode at Sunday, November 11, 2018. The universities may register as sites of the 2019 ICPC Uzbekistan Subregional using this form.

Register the Site

The form for teams registration will be posted later.

P.S. Breaking news: the hosts from Tajikistan and Turkmenistan are welcome to register and participate in Uzbekistan Multi-Site Subregional. Teams from those two countries — time to join ICPC now!

I would like to invite you to participate in the rated Codeforces Round 519 by Botan Investments. Date and time of the round: Oct/28/2018 18:35 (Moscow time).

This is a combined round having 7 problems and lasting 2 hours, and it will be rated.

Tasks for you were prepared by Anadi, Grzmot, isaf27 and Rzepa. Also thanks for:

KAN and cdkrot for help in preparing the problems; --Pavel--, Nerevar, map, GR1n, rutsh, AlexFetisov and winger for testing the round; MikeMirzayanov for Codeforces and Polygon platforms.

The round is supported by Botan Investments.

Prizes! Top 50 participants and 20 random participants with rank from 51 to 500 will receive personalized hoodie with CF handle.

Scoring distribution will be announced later. I wish you a high rating and looking forward to see you at the competition!

UPD: I'll be on the community Discord server shortly after the contest to discuss the problems.

UPD: Scoring: 500 1000 1500 2000 2250 2750 3500

UPD: Editorial

The round is over, congratulations to the winners!

1. scott_wu
2. mnbvmar
3. HIR180
4. ksun48
5. Benq
6. geniucos
7. Alex_2oo8
8. Petr
9. Um_nik
10. V--o_o--V

The Moscow Institute of Physics and Technology welcomes high school students to take part in the programming boot camp Moscow Workshops Juniors! The boot camp will be held from February, 25 to March, 6.

The educational program includes daily studying contests, thematic lectures and practice. In a free time participants could join the popular science lectures, do sports, play the intellectual games and be involved in other activities. According to the results of the introductory contest the participants are divided into divisions depending on their skill level. Participants can choose the most interesting topics and make an appropriate training program. If a participant finds the curriculum too simple or difficult, he can change division.

To take part in the camp, you have to pass qualifying online tours, its format is close to the Olympiad in Informatics. You can participate in several rounds or only in one tour, the ranking of the participants is made according to the results of four rounds. The selection rules can be found by the link.

There are four qualifying rounds:

October, 27 at 16:00 pm UTC+03

November, 18 at 12:00 pm UTC+03

December, 16 at 12:00 pm UTC+03

January, 20 at 12:00 pm UTC+03

Moscow Workshops Juniors suggests awarded high school students several opportunities of participation. If you are a prize-winner of national Olympiads in informatics 2017-2018, you are invited to take part in the Workshops free of charge! For participants of national Olympiads in informatics 2017-2018 the Workshops cost $400, for another participants – $700

REGISTRATION

Have questions still? Write to organizing committee email: [email protected]

On Oct/25/2018 17:35 (Moscow time) Educational Codeforces Round 53 (Rated for Div. 2) will start.

Series of Educational Rounds continue being held as Harbour.Space University initiative! You can read the details about the cooperation between Harbour.Space University and Codeforces in the blog post.

This round will be rated for the participants with rating lower than 2100. It will be held on extented ACM ICPC rules. The penalty for each incorrect submission until the submission with a full solution is 10 minutes. After the end of the contest you will have 12 hours to hack any solution you want. You will have access to copy any solution and test it locally.

You will be given 7 problems and 2 hours to solve them.

The problems were invented and prepared by Roman Roms Glazov, Adilbek adedalic Dalabaev, Vladimir vovuh Petrov, Ivan BledDest Androsov and me.

Good luck to all participants!

Our friends at Harbour.Space also have a message for you:

Hey Codeforces! We want to remind you that the Scholarship for the Master’s in Robotics programme, which starts on January 7th 2019, has an application deadline of November 12th, 2018.

Harbour.Space University and Remy Robotics are collaborating to offer graduate students from anywhere in the world a once in a lifetime opportunity, a fully funded scholarship for Harbour.Space University’s Master’s Programme in Robotics.

The scholarship value is €34.900 and it includes:

• Complete coverage of the University tuition fee (€22,900)

• Internship at Remy Robotics (20h per week during 1 year)

• €1,000 per month during 1 year (Internship earnings)

UPD: vovuh and me will be waiting for you on the community Discord server shortly after the contest to discuss the problems.

Congratulations to the winners:

Congratulations to the best hackers:

And finally people who were the first to solve each problem:

UPD2: Editorial is published