Sometimes I wonder, what implementation of a segment tree to use. Usually, I handwave that some will suit, and that works in most of the cases.

But today I decided to back up the choice with some data and I ran benchmarks against 4 implementations:

• Simple recursive divide-and-conquer implementation
  Code

  struct SimpleRecursiveSegmentTree {
      unsigned size;
  
    private:
      std::vector<long long> t;
  
      void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {
          if (r == l + 1) {
              t[p] = v[l];
              return;
          }
          unsigned m = (l + r) / 2;
          _build(v, 2 * p + 1, l, m);
          _build(v, 2 * p + 2, m, r);
          t[p] = t[2 * p + 1] + t[2 * p + 2];
      }
  
      long long _get(unsigned p, unsigned l, unsigned r, unsigned a,
                     unsigned b) const {
          if (b <= l || r <= a) {
              return 0LL;
          }
          if (a <= l && r <= b) {
              return t[p];
          }
          unsigned m = (l + r) / 2;
          return _get(2 * p + 1, l, m, a, b) + _get(2 * p + 2, m, r, a, b);
      }
  
      void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {
          if (i < l || r <= i) {
              return;
          }
          if (r == l + 1) {
              t[p] += x;
              return;
          }
          unsigned m = (l + r) / 2;
          _add(2 * p + 1, l, m, i, x);
          _add(2 * p + 2, m, r, i, x);
          t[p] = t[2 * p + 1] + t[2 * p + 2];
      }
  
    public:
      SimpleRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {
          t.resize(4 * size);
      }
  
      SimpleRecursiveSegmentTree(const std::vector<int> &v) noexcept
          : size(v.size()) {
          t.resize(4 * size);
          _build(v, 0, 0, size);
      }
  
      void add(unsigned i, int x) { _add(0, 0, size, i, x); }
  
      long long get(unsigned l, unsigned r) const {
          return _get(0, 0, size, l, r);
      }
  };
  

• Optimized recursive divide-and-conquer, which does not descend into apriori useless branches
  Code

  struct OptimizedRecursiveSegmentTree {
      unsigned size;
  
    private:
      std::vector<long long> t;
  
      void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {
          if (r == l + 1) {
              t[p] = v[l];
              return;
          }
          unsigned m = (l + r) / 2;
          _build(v, 2 * p + 1, l, m);
          _build(v, 2 * p + 2, m, r);
          t[p] = t[2 * p + 1] + t[2 * p + 2];
      }
  
      long long _get(unsigned p, unsigned l, unsigned r, unsigned a,
                     unsigned b) const {
          if (a <= l && r <= b) {
              return t[p];
          }
          unsigned m = (l + r) / 2;
          long long res = 0;
          if (a < m) {
              res += _get(2 * p + 1, l, m, a, b);
          }
          if (b > m) {
              res += _get(2 * p + 2, m, r, a, b);
          }
          return res;
      }
  
      void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {
          if (r == l + 1) {
              t[p] += x;
              return;
          }
          unsigned m = (l + r) / 2;
          if (i < m) {
              _add(2 * p + 1, l, m, i, x);
          } else {
              _add(2 * p + 2, m, r, i, x);
          }
          t[p] = t[2 * p + 1] + t[2 * p + 2];
      }
  
    public:
      OptimizedRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {
          t.resize(4 * size);
      }
  
      OptimizedRecursiveSegmentTree(const std::vector<int> &v) noexcept
          : size(v.size()) {
          t.resize(4 * size);
          _build(v, 0, 0, size);
      }
  
      void add(unsigned i, int x) { _add(0, 0, size, i, x); }
  
      long long get(unsigned l, unsigned r) const {
          return _get(0, 0, size, l, r);
      }
  };
  

• Non-recursive implementation (credits: https://codeforces.net/blog/entry/18051)
  Code

  struct NonRecursiveSegmentTree {
      unsigned size;
  
    private:
      std::vector<long long> t;
  
      void _build(const std::vector<int> &v) {
          std::copy(v.begin(), v.end(), t.begin() + size);
          for (int i = size - 1; i > 0; --i) {
              t[i] = t[i * 2] + t[i * 2 ^ 1];
          }
      }
  
    public:
      NonRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {
          t.resize(2 * size);
      }
  
      NonRecursiveSegmentTree(const std::vector<int> &v) noexcept
          : size(v.size()) {
          t.resize(2 * size);
          _build(v);
      }
  
      void add(unsigned i, int x) {
          i += size;
          for (t[i] += x; i > 1; i /= 2) {
              t[i / 2] = t[i] + t[i ^ 1];
          }
      }
  
      long long get(unsigned l, unsigned r) const {
          long long res = 0;
          for (l += size, r += size; l < r; l /= 2, r /= 2) {
              if (l & 1) {
                  res += t[l++];
              }
              if (r & 1) {
                  res += t[--r];
              }
          }
          return res;
      }
  };
  

• Fenwick Tree
  Code

  struct FenwickTree {
      unsigned size;
  
    private:
      std::vector<long long> t;
  
      long long get_prefix(int i) const {
          long long res = 0;
          while (i >= 0) {
              res += t[i];
              i = (i & (i + 1)) - 1;
          }
          return res;
      }
  
    public:
      void add(unsigned i, int x) {
          while (i < size) {
              t[i] += x;
              i = i | (i + 1);
          }
      }
  
      FenwickTree(unsigned _size) : size(_size) { t.resize(size); }
  
      FenwickTree(const std::vector<int> &v) : size(v.size()) {
          t.resize(size);
          for (unsigned i = 0; i < size; ++i) {
              add(i, v[i]);
          }
      }
  
      long long get(unsigned l, unsigned r) {
          return get_prefix((int)r - 1) - get_prefix((int)l - 1);
      }
  };
  

All implementations are able to:

• get(l, r): get sum on a segment (half-interval) $$$[l; r)$$$
• add(i, x): add $$$x$$$ to the element by index $$$i$$$

Here are the results: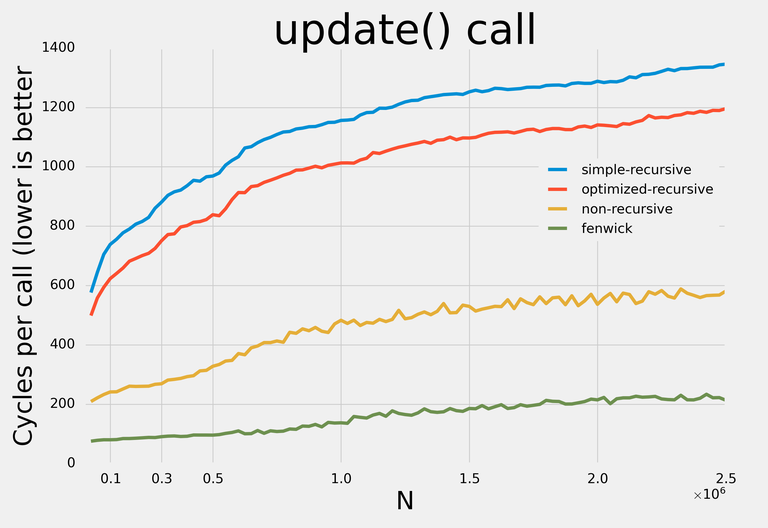

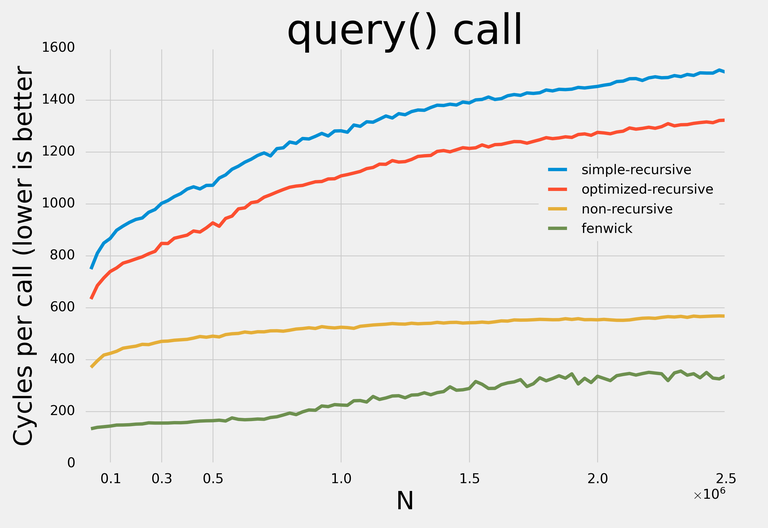
Note: I decided not to apply any addition-specific optimizations so that with minor modifications the data structures could be used for any supported operations.

I generated queries the following way:

• Update: generate random index (rnd() % size) and number
• Query: at first, generate random length (rnd() % size + 1), then generate a left border for that length

Benchmarking source code. Note that ideally you should disable frequency scaling and close any applications that might disrupt the benchmark (basically, the more you close — the better).

Plot-generating Python script

My benchmarking data in case you want to do some more plotting/comparing.

I compiled the benchmark with #pragma GCC optimize("O3") on GNU GCC 11.3.0, and ran it with the CPU fixed on 2.4 GHz without the desktop environment open.

This is probably my first useful contribution so any suggestions/improvements are welcome.