Иногда я задумываюсь, какую реализацию дерева отрезков написать в задаче. Обычно я при помощи метода "пальцем в небо" выбираю какую-то и в большинстве случаев она проходит ограничения.
Я решил подвести основу, так сказать базу, под этот выбор и протестировал на производительность 4 разные реализации:
- Простой рекурсивный "Разделяй и властвуй" Код
- Оптимизированный рекурсивный "Разделяй и властвуй", который не спускается в заведомо ненужных сыновей. Код
- Нерекурсивная реализация (взял отсюда: https://codeforces.net/blog/entry/18051) Код
- Дерево Фенвика Код
Все реализации поддерживают такие запросы:
-
get(l, r): сумма на отрезке (полуинтервале) $$$[l; r)$$$ -
update(i, x): прибавление к элементу под индексом $$$i$$$ числа $$$x$$$
Вот результаты: 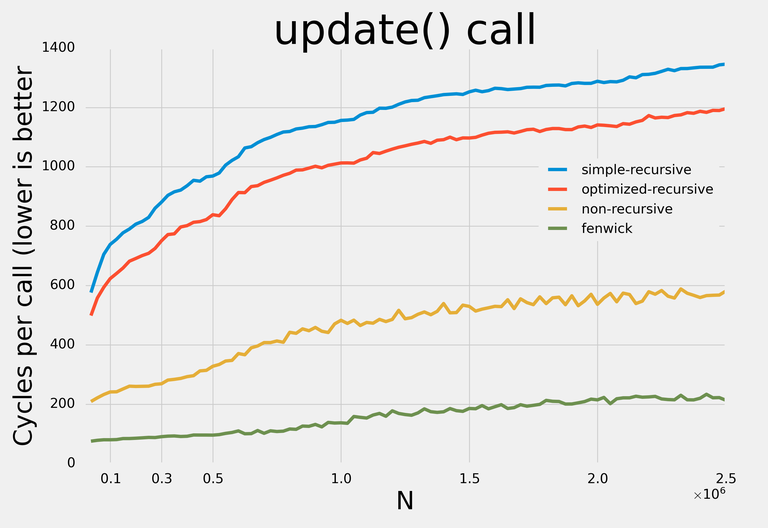
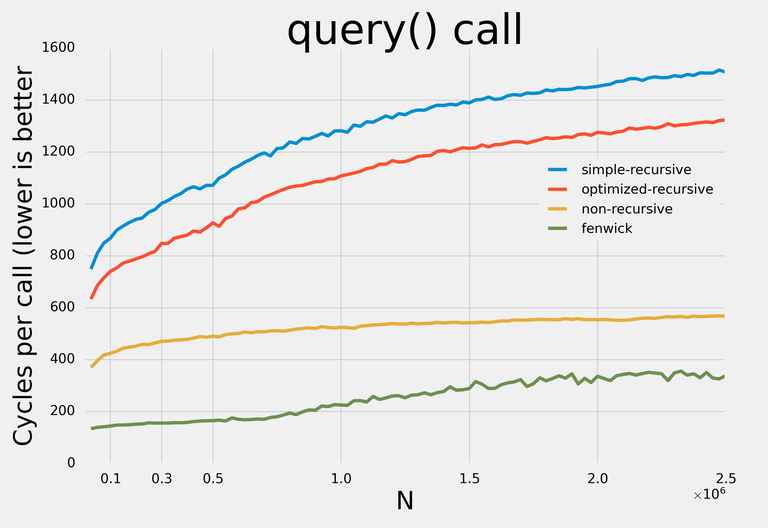
Примечание: я старался не делать никаких оптимизаций, требовательных к конкретным запросам, чтобы с небольшими изменениями структуры данных могли применяться для любых операций.
Я генерировал запросы следующим образом:
- Прибавление в точке: случайный индекс (
rnd() % size) и случайное число - Сумма на отрезке: сначала, генерируется длина отрезка (
rnd() % size + 1), затем подходящая левая граница.
Исходники бенчмарка. Примечание: желательно отключить CPU frequency scaling и закрыть все приложения, которые могут мешать бенчмарку (чем больше закроете -- тем в теории стабильнее будет результат).
Скрипт на Python, создающий красивый график
Результаты в формате JSON на случай, если Вы захотите ещё поиграться с данными.
Я компилировал бенчмарк с #pragma GCC optimize("O3") на GNU GCC 11.3.0 и запускал его с фиксированной частотой процессора 2.4 GHz.
Наверное, это мой первый вклад в сообщество, поэтому любые дополнения/предложения приветствуются.







