Actually, I'm writing this because it took me about 34 minutes to solve this problem 495A - Цифровой индикатор And after I solved it, I saw that everyone's solutions are much shorter than mine

Well the problem hint is to count how many other digits can be constructed by adding some sticks to the x Digit For example, if X=3, So you can construct 3 (Adding 0 Sticks)

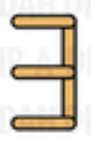
8 (Adding 2 Sticks)

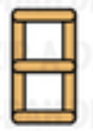
9 (Adding 3 Sticks)

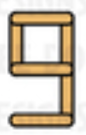
So for x=3, you can construct 3 other digits (3,8,9)

Well you count for all other digits (from 0, 1, 2.... to 9) in the same way

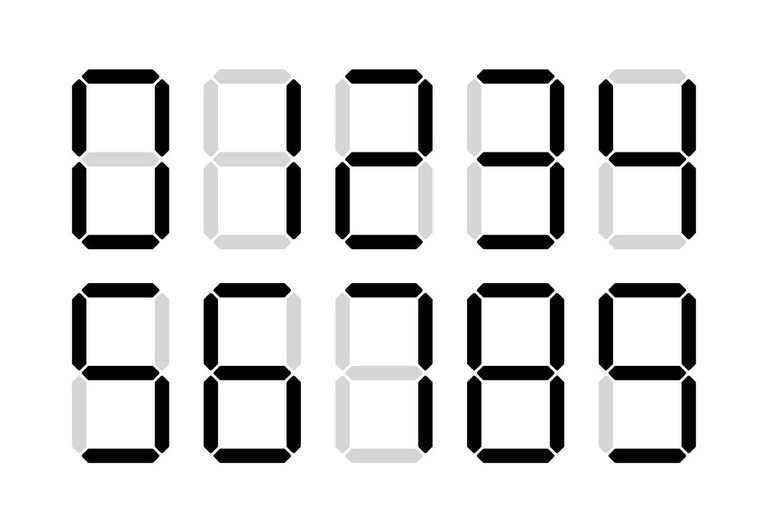
Well I saw people counted the values and filled them in an array like so

#include<bits/stdc++.h>
using namespace std;
int main() {
	ll n, d[10] = { 2, 7, 2, 3, 3, 4, 2, 5, 1, 2 };
	cin >> n;
	cout << d[n / 10] * d[n % 10];
}

But in fact, I prefer to count them using the code (Bruteforce) because I do not trust myself (Maybe while I am counting them with my eyes or trying to imagine them. I may miss something)

So Here is What I did, I wrote a program to count them for me, and fill the results in a map or an array

First I numbered each stick and thend saved the indexes in a vector so (Not a hard task)

v[Digit] = {Number of Sticks' indices}

And I did the same thing for the rest of the digits

bool vecInVec(vector<int>v1, vector<int>v2) {
	for (auto i : v1) 
		if (find(begin(v2), end(v2), i) == end(v2)) return 0;
	return 1;
}
map<int, int>cal() {
	vector<vector<int>>v(10);
	v[0] = { 1,2,3,5,6,7 };
	v[1] = { 3,7 };
	v[2] = { 2,3,4,5,6 };
	v[3] = { 2,3,4,6,7 };
	v[4] = { 1,3,4,7 };
	v[5] = { 1,2,4,6,7 };
	v[6] = { 1,2,4,5,6,7 };
	v[7] = { 2,3,7 };
	v[8] = { 1,2,3,4,5,6,7 };
	v[9] = { 1,2,3,4,6,7 };
	map<int, int>mp;
	for (int i = 0; i < 10; i++) {
		for (auto all : v) {
			if (vecInVec(v[i],all))mp[i]++;
		}
	}
	return mp;
}

Well to count how many digits can be constructed by adding sticks, you search for digits has the same sticks, so in coding, I counted the number of vectors have the same indexes

In fact, that code showed me the results accurately.. and I did not need much time to review it.. The only time it took was to count the stick's indices.. and this is much easier than counting the digits that can be built from other digits

0 : 2
1 : 7
2 : 2
3 : 3
4 : 3
5 : 4
6 : 2
7 : 5
8 : 1
9 : 2

Here is the submission link in case you want to see it 177933751

Well to in summary.. This is a longer code, but it is more useful.. Today you learned a way to make the computer think and count with you instead of manual counting (which may be inaccurate).. This is an opinion I will be glad to know your opinions, whether you agree or disagree. Leave me a comment