Answer is $$$floor(sqrt(r)) — floor(sqrt(l — 1))$$$.

Alternatively you can use binary search to calculate square root.

You always can make all bits less or equal to the most significant bit set to $$$1$$$. Also you cant make most significant bit greater.

Just go through numbers and find the minimal most significant bit.

Answer is number with all bits less or equal to minimal most significant bit set to $$$1$$$.

Best way to choose the integer is the $$$gcd$$$ of all elements in the array except for element you want to change.

So you just need to calculate the $$$gcd$$$ of all elements in the array except for one in some fast way.

You can use pre-calculated prefix/suffix $$$gcd$$$ to do it.

Also take care about the case $$$n = 1$$$, The answer for this case will be always $$$10^9$$$.

We can imagine that Alice and Bob are on different sides of the river. It's obvious that in this case best path is just straight line between Alice and Bob.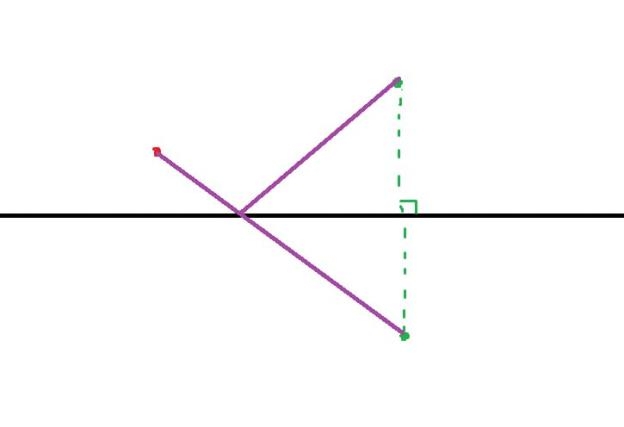

So you can just negate $$$y$$$ coordinate for Bob and calculate the Euclidean distance of the obtained point with the other point, It can be proven that the obtained distance is the shortest possible

It's obvious that you can change bases in original formula to their last digits.

After you can just check some cases.

$$$1^{10x+1}$$$ mod $$$10$$$ is always $$$1$$$
$$$2^{10x+2}$$$ mod $$$10$$$ is switching between $$$4$$$ and $$$6$$$
$$$3^{10x+3}$$$ mod $$$10$$$ is switching between $$$7$$$ and $$$3$$$
$$$4^{10x+4}$$$ mod $$$10$$$ is always $$$6$$$
$$$5^{10x+5}$$$ mod $$$10$$$ is always $$$5$$$
$$$6^{10x+6}$$$ mod $$$10$$$ is always $$$6$$$
$$$7^{10x+7}$$$ mod $$$10$$$ is switching between $$$3$$$ and $$$7$$$
$$$8^{10x+8}$$$ mod $$$10$$$ is switching between $$$6$$$ and $$$4$$$
$$$9^{10x+9}$$$ mod $$$10$$$ is always $$$9$$$
$$$0^{10x+0}$$$ mod $$$10$$$ is always $$$0$$$

If you already calculated answer for $$$n$$$ — $$$1$$$, you can find answer for $$$n$$$ in next way:

You already have calculated answer for all subsets without $$$n$$$.

Now you want to find answer for all new subsets.

It's obvious that all new subsets are old subsets but with $$$n$$$ in them.

So for all subsets you want to go from $$$\frac{f}{s}$$$ to $$$\frac{f + n)}{(s * n)}$$$.

$$$\frac{f + n}{s * n} = \frac{f}{s}{n} + \frac{n}{s}{n} = $$$\frac{old_answer}{n} + $$$\frac{1}{s}$$$.

So you want to keep sum of 1/s ans sum of answers for all subsets

Let sum of 1/s be Y and sum of answers be X

When you add n, Y changes to Y + Y/n, and X changes to X + X/n + Y

Final answer is X