Consider the following problem :

Your are given an array $$$a$$$ of size $$$n$$$ and $$$q$$$ queries of form $$$(l_1, r_1), (l_2, r_2), ..., (l_q, r_q)$$$. For each query you have to find the MEX of the array $$$a_l, a_{l+1}, ..., a_r$$$. The queries are offline.

$$$0 \le a_1, a_2, ..., a_n \le n$$$

$$$1 \le l_i \le r_i \le n$$$, for all $$$1 \le i \le q$$$

The approach to the problem is discussed here.

First let's consider a special case of the queries where $$$r = n$$$. In this case we want to find the smallest integer that does not occur in the subarray $$$a_l, ..., a_r$$$. That is, the smallest integer that does not occur at index $$$l$$$ or after it.

For all $$$0 \le x \le n$$$, let $$$b_x$$$ be the greatest index $$$i$$$ such that $$$a_i = x$$$, and $$$0$$$ if no such $$$a_i$$$ exists.

Now the MEX say $$$m$$$ of subarray $$$a_l, ..., a_n$$$ either does not occur in $$$a$$$, in which case we have $$$b_m = 0$$$, or the last occurence of $$$m$$$ in $$$a$$$ is before $$$l$$$, thus $$$b_m < l$$$. We can say that $$$m$$$ is the minimum of all such numbers, thus $$$m$$$ = $$$min$$$ { $$$i$$$ | $$$b_i < l$$$ }.

Now since the queries are offline, we can sort the queries by $$$r$$$ and process them such that we can ignore the subarray $$$a_{r + 1}, ..., a_n$$$. We iterate from from $$$r = 1, 2, ..., n$$$, and for each $$$r$$$ we process all queries $$$(l_i, r_i)$$$ where $$$r_i = r$$$.

Now how do we efficiently calculate the answer for queries $$$(l, n)$$$ ?

We maintain a minimum segment tree on the array $$$b$$$ and update all values for $$$i = 1, 2, ..., r$$$. Now since there are $$$n$$$ updates but $$$n + 1$$$ leaf nodes in the segment tree, at least one of them is zero. So value of root node is $$$0$$$. Now we try to find the minimum index leaf node with value < $$$l$$$. We start at root node and travel down to this node. At each node we see if the value of it's left child is < $$$l$$$. If it is we go to left child. Otherwise we go to the right child. Either of left or right child will always have value < $$$l$$$. Finally we reach a leaf node, the index of this node(after adjusting for offset) is the mex of array $$$a_l, a_{l + 1}, ..., a_r$$$.

Consider the array $$$a = [6, 1, 0]$$$

Consider evaluation for $$$l = 2, r = 3$$$. The subarray is $$$[a_2, a_3] = [1, 0]$$$.

We see that the left child has value < $$$l$$$.

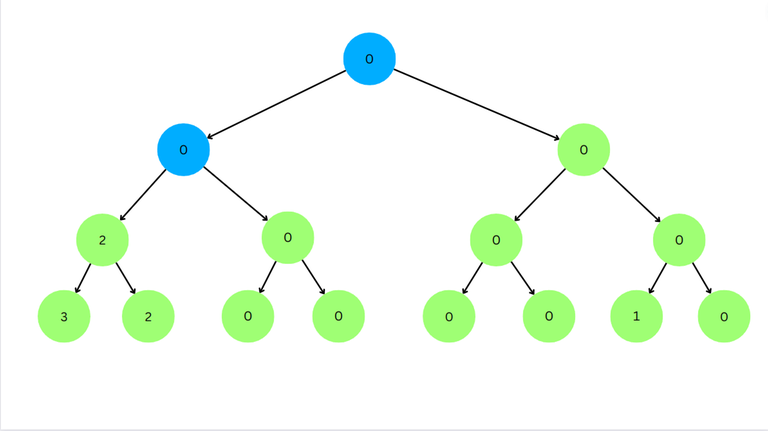
Now for left node $$$2 \ge l$$$. So we go to right node.

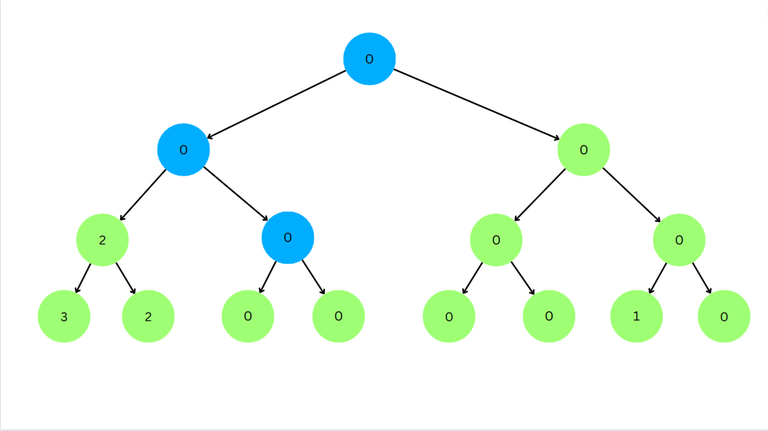
Now for the left child value < $$$l$$$. So we go to left child.

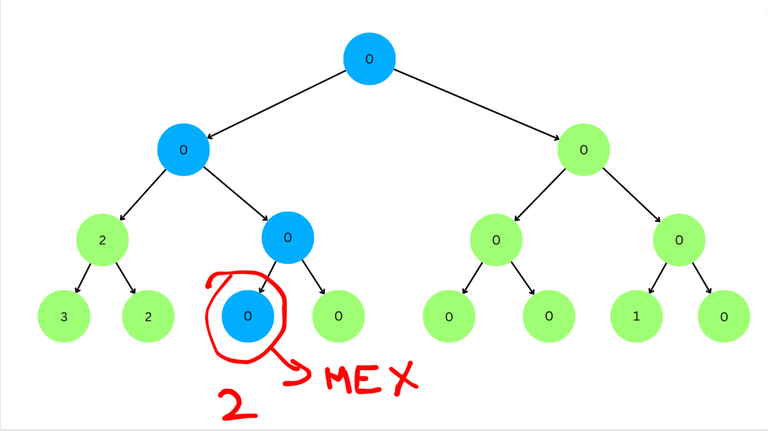
We have reached a leaf node. The corresponding index is 2 and thus the MEX of the subarray $$$a_2, a_3$$$ is 2.

Calculating MEX of each query takes $$$O(log n)$$$ time, total $$$O(q log n)$$$. Updating the tree for $$$b$$$ takes $$$O(n log n)$$$ time in total. Sorting $$$q$$$ queries takes $$$O(q log q)$$$ time.

Overall time complexity — $O(nlog n + q(log n + log q))

#include<bits/stdc++.h>
using namespace std;
#define ll long long
struct SegmentTree{
    int n;
    vector<int> tree;
    SegmentTree(int sz){
        n = 1;
        while(n < sz){
            n <<= 1;
        }
        tree.assign(2 * n, 0);
    }
    void set(int ind, int val){
        ind += n;
        tree[ind] = val;
        ind >>= 1;
        while(ind > 0){
            tree[ind] = min(tree[2 * ind], tree[2 * ind + 1]);
            ind >>= 1;
        }
    }
    int get(int x){
        // return the first index i, such that s[i] < x
        int node = 1;
        while(node < n){
            int left = (node << 1);
            int right = (node << 1) + 1;
            if(tree[left] < x){
                node = left;
            }else{
                node = right;
            }
        }
        return (node - n);
    }
};
int main(){
    int n;
    cin >> n;
    vector<int> a(n + 1);
    for(int i = 1; i <= n; ++i){
        cin >> a[i];
    }
    int q;
    cin >> q;
    vector<vector<pair<int, int>>> queries(n + 1);
    for(int i = 0; i < q; ++i){
        int l, r;
        cin >> l >> r;
        queries[r].push_back({l, i});
    }

    vector<int> res(q);

    SegmentTree s(n + 1);
    for(int i = 1; i <= n; ++i){
        // set the last occurence of a[i] to i
        s.set(a[i], i);

        for(auto [l, ind] : queries[i]){
            // find the smallest x, such that last occurence of x < l
            res[ind] = s.get(l);
        }
    }
    for(int elem : res){
        cout << elem << '\n';
    }
    cout << '\n';

    return 0;
}