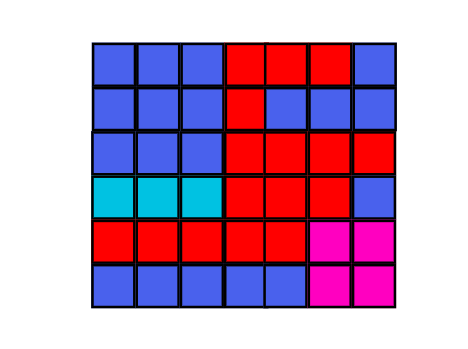
Question: You have a $$$N * M$$$ matrix. The color of cell in $$$i^{th}$$$ row and $$$j^{th}$$$ column is $$$a_{ij}$$$. Find the number of rectangles that can be formed from this matrix by deleting some rows and columns, that have all cells of same color.

Idea: Let $$$i_l, j_l$$$ be the coordinates of the top left corner and $$$i_r, j_r$$$ be the coordinates of the bottom right corner. We can see that $$$(i_l, j_l, i_r, j_r)$$$ uniquely define a rectangle.

Let's call a rectangle valid if it has all cells of same color.

Now let $$$dp[i][j]$$$ be the number of valid rectangles with their bottom right corner at $$$(i, j)$$$.

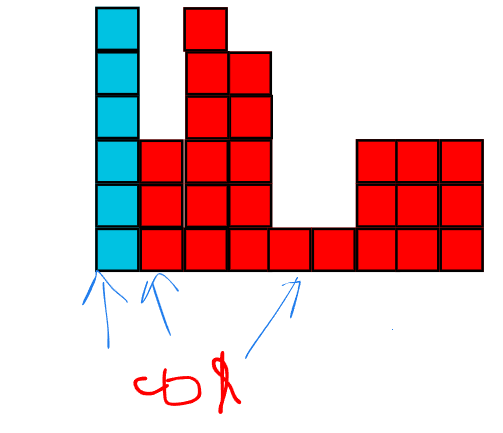
Let $$$h[i][j]$$$ be the "height" of columns at $$$(i, j)$$$. That is

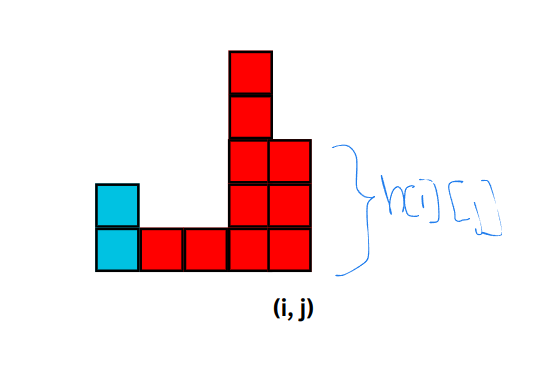
$$$h[i][j]$$$ = max value of $$$len$$$ such that $$$a[i][j] = a[i][t]$$$ , for all $$$t = i - len + 1, i - len + 2, ..., i$$$.

How do we computer $$$dp[i][j]$$$ efficiently ?

Consider how $$$dp[i][j]$$$ depends on $$$dp[i-1][j], dp[i - 2][j], ...$$$.

For some $$$k, k < j$$$, if $$$a[i][k] != a[i][j]$$$, then $$$dp[i][k]$$$ will make no contribution to $$$dp[i][j]$$$. So let's assume that $$$a[i][t] = a[i][j]$$$ for all $$$t = k, k + 1, ..., j$$$.

Now what is the maximum height of rectangle with bottom right corner at $$$(i, j)$$$ and top left corner in the column $$$k$$$ ?

It is $$$height_k = min_{k \le t \le i}(h[i][t])$$$. Then then the number of such rectangles is $$$height_k$$$, since we can have rectangles of height $$$1, 2, 3, ..., height_k$$$.

Also consider that if $$$h[i][k] \le height_k$$$, then for any rectangle with bottom right corner at $$$(i, k)$$$ can be extended so that it has bottom right corner at $$$(i, j)$$$.

Let $$$k$$$ be the first index such that $$$a[i][k] = a[i][j]$$$ and $$$h[i][k] < h[i][j]$$$.

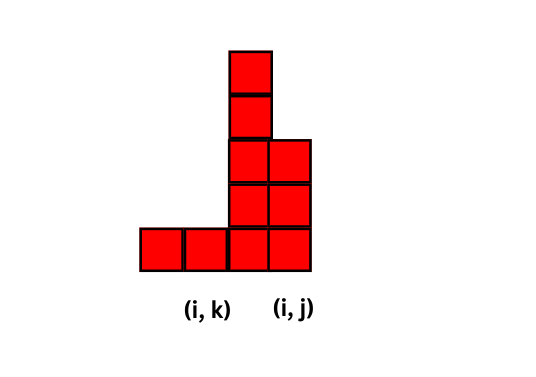
Then every rectangle with bottom right corner at $$$(i, k)$$$ can be extended to $$$(i, j)$$$. Also the height of any rectangle with top-left corner after $$$(i, k)$$$ is at most $$$h[i][j]$$$, since by definition for any $$$t, k < t \le i$$$ we have $$$h[i][t] \ge h[i][j]$$$.

Thus the number of rectangles after k are $$$h[i][j] * (j - k)$$$.

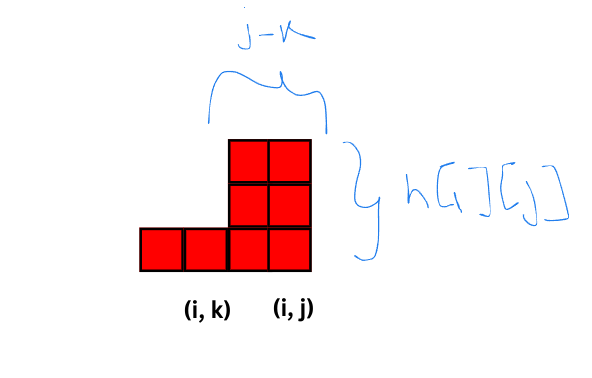
Thus we have, $$$dp[i][j] = dp[i][k] + h[i][j] * (j - k)$$$.

Now the question is how do we efficiently find $$$k$$$ ?

We can do this by maintaining an array of indices $$$col$$$ such that $$$h[i][col] < min_{t < col}(h[i][t])$$$.