Edit 25.09.2024
Thanks to dsogari's for pointing out in the comments a clever solution to this problem that makes for a fast and simple algorithm ($$$O(n)$$$ time, $$$O(1)$$$ space):
The solution described in this post is longer and more constructive. While I like the short version, I also think the constructive approach has some merit since it produces not only the answer, but the final state of the array and a series of transformations to get there.
Also check out Orn0's post about his solution to this problem using binary search on answer, complete with detailed mathematical proofs.
Overall it's been a very engaging problem with a simple and clear statement, and lots of approaches to a solution. It led to extensive discussions and at least 2 blog posts dedicated to it :) So again, big thanks to soullless, Wansur and Chalishkan for introducing it.
Original post
I recently decided to realize my long standing dream of becoming better at contest coding. My current goal is to enter div1. In a recent contest I got stuck on a problem D. After solving A, B and C I had more than an hour to solve D. It took me overall extra 3-4 hours after the contest to figure out the details and finally code the working solution. Problems like this are my current hurdle, and the ability to solve them quickly during the round is what I'd like to obtain.
As a part of that journey, I decided to write a detailed explanation for the solution of the problem that defeated me during the round, along with my train of though when solving it. I appreciate any comments, advice, thoughts on how to solve these problems and alternative points of view. I had fun writing it, so I'm thinking of making a habit of doing it for problems that I get stuck on.
Statement
Your are given an array $$$a_1,a_2,\ldots,a_n$$$ of the length $$$n$$$. You can perform any number (possibly, zero) of operations on the array.
In one operation, we choose a position $$$i$$$ ($$$1\leq i\leq n−1$$$) and perform the following action: $$$a_i := a_i − 1$$$ , and $$$a_i + 1 := a_i + 1$$$
Find the minimum possible value of $$$\max(a_1,a_2,\ldots,a_n)−\min(a_1,a_2,\ldots,a_n)$$$.
Solution walk-through
First, let's to conceptualize the elements of the array as columns of blocks. Then our given action is equivalent to moving a block from the left column to the right column.
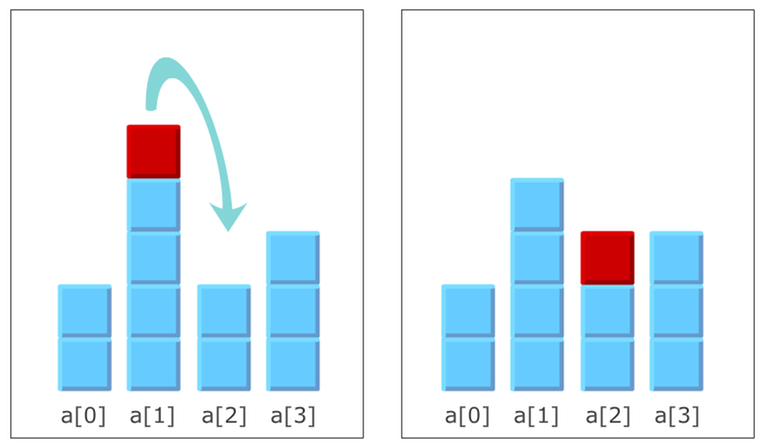
By repeating this action we can now move any amount of blocks from left to right and distribute them as we want. 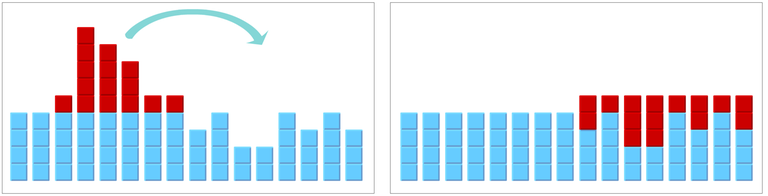
So how do we approach the solution? I started as we do with dynamic programming problems: suppose we already have a solution for a subarray and try to extend it for a larger subarray. It seemed promising to go from right to left. Suppose we have a solution for the suffix subarray $$$[a_{i+1},\ldots,a_n]$$$, how do we use it to get a solution for a larger suffix $$$[a_{i},\ldots,a_n]$$$?
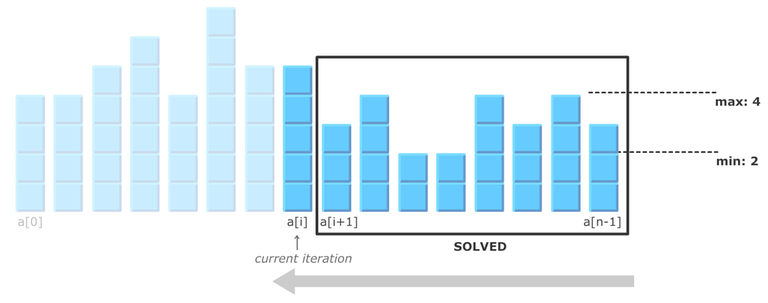
Here's how we might do the iteration step:
if $$$a_i$$$ is less than or equal the current minimum, then $$$a_i$$$ becomes the new minimum (or joins existing minimums). There's nothing we can do about it, because taking anything from $$$a_i$$$ makes it even smaller. This is the simplest case.
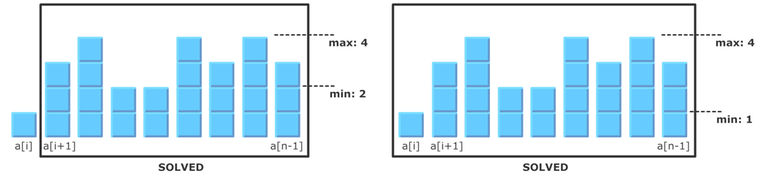
if $$$a_i$$$ is greater than the current minimum, then it has something to offer. We can take the excess amount from $$$a_i$$$ and redistribute it in the array to improve the situation. One obvious (but impractical) strategy would be to take one block from the excess and place it on the current minimum, then repeat while there still remains some excess. The question is now, how to do that efficiently.
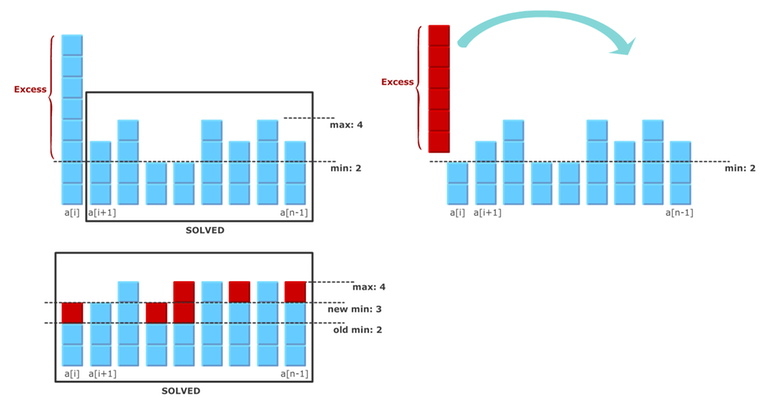
So we got the outline of the algorithm:
Consider $$$a[i]$$$ going from right to left;
For each $$$a[i]$$$ remove the excess and redistribute the it to minimize the target function.
If implemented directly, by moving blocks one by one, this will cost $$$O\left(n\cdot\sum a_i\right)$$$.
To get to the proper efficiency there's one more crucial consideration: when we do the iteration step and remove the excess from the $$$a_i$$$ element, it becomes the new minimum (or one of the minimums). As we have control over where to redistribute the excess, we can choose to keep $$$a_i$$$ minimum. This means, that we can keep the solved subarray always in a non-descending order. 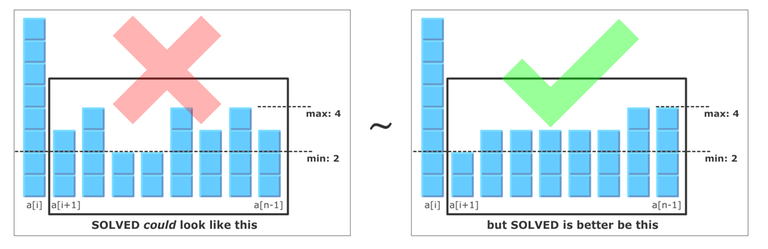
First, this removes the need to keep track of minimums. But more importantly, the excess redistribution strategy becomes more clear. 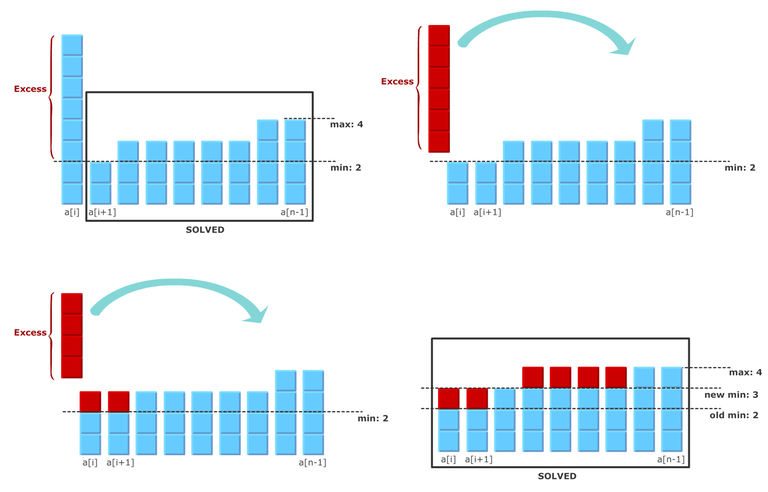
Since all the minimums are grouped together now, we can increase them simultaneously, until they reach the next height. We can do this iteratively by finding the available rectangular space and filling it with excess. If all the elements on the right are equal, we can say that the available space is infinite. 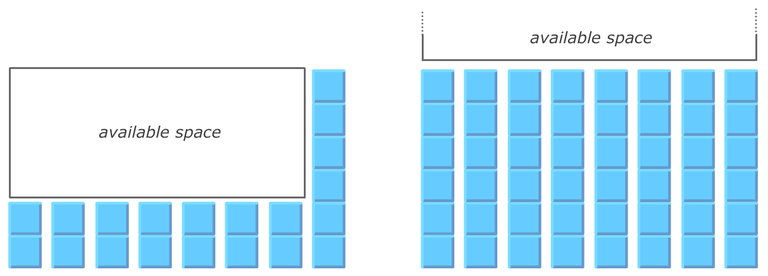
If excess >= space, then we fill the space completely, reduce the excess by the space, and continue the process. 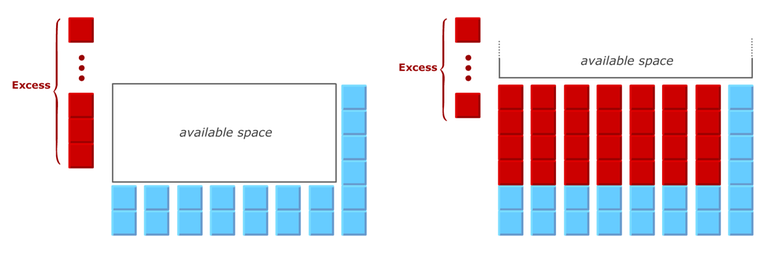
If excess < space, then we distribute it as uniformly as possible, leaving larger columns on the right side. 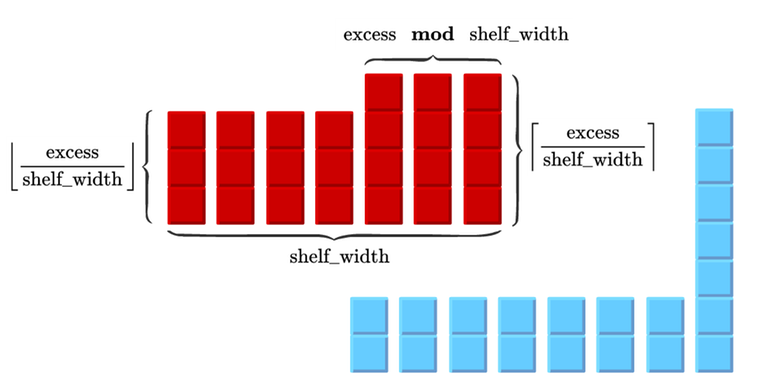
Doing this is still $$$O(n^2)$$$, because on each iteration we have to update (in the worst case) all the elements on the right.
The final improvement is to represent the right side suffix array as a collection of shelves, and treat this collection as a stack where on top of the stack lies the leftmost shelf. 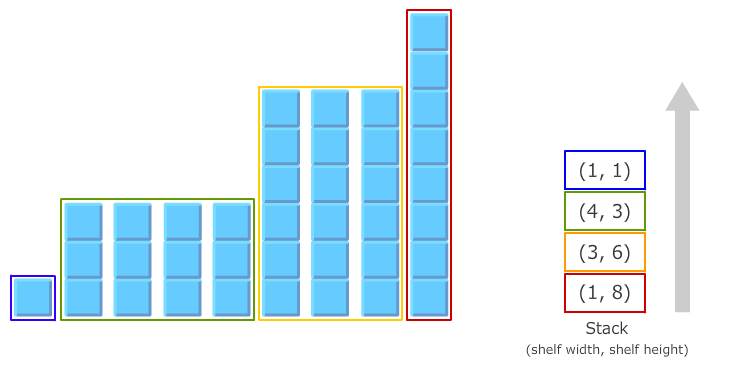
On each iteration shelves are transformed in the following manner:
if
space <= excess, then we pop the top shelf, widen the next shelf, reduce the excess by space and repeat.if
space > excess(or there's only one shelf on the stack), then we rearrange the excess, making at most one new shelf.
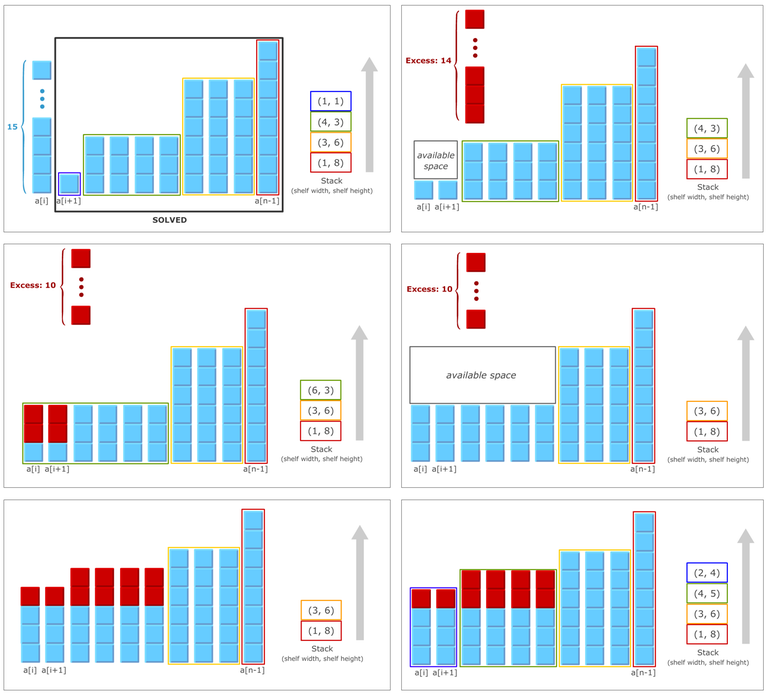
So each iteration stack grows by at most one element. On a given iteration the stack can shrink by arbitrary amount, but the total amount of decreases can't be more than the the total amount of increases. So this gives us amortized complexity of $$$O(1)$$$ stack operations per iteration, resulting in $$$O(n)$$$ per input.
The final answer can be obtained as a difference between the height of the rightmost shelf and the leftmost shelf (bottom of the stack shelf and the top of the stack shelf).
My implementation in C++:
struct Shelf {
INT width;
INT height;
};
INT GetSpace(const Vec<Shelf>& stack) {
if (stack.size() < 2) {
return std::numeric_limits<INT>::max();
}
Shelf shelf = stack[stack.size() - 1];
Shelf next_shelf = stack[stack.size() - 2];
INT diff = next_shelf.height - shelf.height;
return diff * (shelf.width + 1);
}
INT Solve(Vec<INT>& arr) {
Vec<Shelf> stack;
stack.emplace_back(1, arr.back());
for (int i = arr.size() - 2; i >= 0; --i) {
Shelf shelf = stack.back();
if (arr[i] < shelf.height) {
stack.emplace_back(1, arr[i]);
continue;
}
INT excess = arr[i] - shelf.height;
INT space = GetSpace(stack);
stack.pop_back();
while (space <= excess) {
stack.back().width += shelf.width;
excess -= space;
shelf = stack.back();
space = GetSpace(stack);
stack.pop_back();
}
INT div = excess / (shelf.width + 1);
INT rem = excess % (shelf.width + 1);
if (rem > 0) {
stack.emplace_back(rem, shelf.height + div + 1);
}
stack.emplace_back(shelf.width + 1 - rem, shelf.height + div);
}
return stack.front().height - stack.back().height;
}
Checker algorithm for brute-force testing
When implementing the solution I made several mistakes in handling shelf merges and splits. In order to catch those and find inputs for which my solution breaks, I implemented a simple $$$O(n^2)$$$ algorithm than scans the array and for each pair of neighboring columns regresses them to the mean if possible: - if $$$a_i>a_{i+1}$$$, then $$$a_i:=\lfloor (a_i+a_{i+1})/2 \rfloor$$$ and $$$a_{i+1}:=\lceil (a_i+a_{i+1})/2 \rceil$$$. Continue the scan until no changes have been made.
INT SolveBrute(vector<INT>& arr) {
bool changed = true;
while (changed) {
changed = false;
for (int i = arr.size() - 2; i >= 0; --i) {
if (arr[i] > arr[i + 1]) {
changed = true;
INT sum = arr[i] + arr[i + 1];
arr[i] = sum / 2;
arr[i + 1] = arr[i] + sum % 2;
}
}
}
return arr[arr.size() - 1] - arr[0];
}
Now I can test my solution against the slower algorithm on every combination of inputs to find bugs.
The advantage of this algorithm as a checker is that it's simple and short. Although I am unsure how to prove it's correctness. Any thoughts and ideas on that would be greatly appreciated.
Thank you for reading, hope it was clear enough and useful!






