#	User	Rating
1	jiangly	3976
2	tourist	3815
3	jqdai0815	3682
4	ksun48	3614
5	orzdevinwang	3526
6	ecnerwala	3514
7	Benq	3482
8	hos.lyric	3382
9	gamegame	3374
10	heuristica	3357

#	User	Contrib.
1	cry	169
2	-is-this-fft-	165
3	atcoder_official	160
3	Um_nik	160
5	djm03178	157
6	Dominater069	156
7	adamant	153
8	luogu_official	152
9	awoo	151
10	TheScrasse	147

Apologize for my bad English.

We consider to make the answer with a fixed $$$x=2^{p_1}3^{p_2}5^{p_3}...$$$. It's $$$\prod^i{C_{x+p_i-1}^p_i}=\prod^i{\frac {x(x+1)(x+2)...(x+p_i-1)}{p_i!}}$$$ and is already proved in many editorials. Note that it's a polynomial of $$$x$$$, and it's highest exponent is no more than $$$\lfloor\log 2\times 10^5\rfloor = 16$$$.

To calculate the answer, we should know the value of $$$\sum_{i=0}^x i^d$$$. Actually, we have an equation:

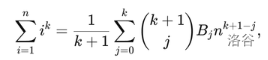
From Chinese OI-wiki, where $$$B_i$$$ stands for the i-th Bernoulli's Number.

Thus, we can solve the problem in $$$k\log^2 k$$$ time. Very slow, bro!

Code:

...

include <bits/stdc++.h>

using namespace std;

define int long long

define M 998244353

constexpr int MAXN = 18; int B[MAXN], C[MAXN][MAXN], inv[MAXN];

define N 200005

vector ex[N];

void init() { for (int i = 0; i < MAXN; i++) { C[i][0] = C[i][i] = 1; for (int k = 1; k < i; k++) C[i][k] = (C[i — 1][k] % M + C[i — 1][k — 1] % M) % M; } inv[1] = 1; for (int i = 2; i < MAXN; i++) inv[i] = (M — M / i) * inv[M % i] % M; B[0] = 1; for (int i = 1; i < MAXN; i++) { int ans = 0; if (i == MAXN — 1) break; for (int k = 0; k < i; k++) ans += C[i + 1][k] * B[k], ans %= M; ans = (ans * (-inv[i + 1]) % M + M) % M; B[i] = ans; } for (int i = 2; i < N; i++) { int d = i, cur = 0; for (int j = 2; j * j <= d; j++) { cur = 0; while (d % j == 0) cur++, d /= j; if (cur) ex[i].push_back(cur); } if (d > 1) ex[i].push_back(1); } }

define Lim 40005

int b1[MAXN][Lim], b2[MAXN][Lim];

void pwinit() { for (int i = 1; i < MAXN; i++) { b1[i][0] = b2[i][0] = 1; for (int j = 1; j < Lim; j++) b1[i][j] = b1[i][j — 1] * i % M; b2[i][1] = b1[i][Lim — 1] * i % M; for (int j = 2; j < Lim; j++) b2[i][j] = b2[i][j — 1] * b2[i][1] % M; } }

int qpow(int a, int t) { if (a < MAXN) return b1[a][t % Lim] * b2[a][t / Lim] % M; if (!t) return 1; if (t == 1) return a; int x = qpow(a, t / 2); x = x * x % M; if (t & 1) x = x * a % M; return x; } int poly[MAXN], tmp[MAXN];

void mul(int k) { for (int i = 0; i < MAXN; i++) tmp[i] = poly[i] * k % M; for (int i = 1; i < MAXN; i++) tmp[i] = (poly[i — 1] + tmp[i]) % M; for (int i = 0; i < MAXN; i++) poly[i] = tmp[i]; }

int calc(int x, int lim) { memset(poly, 0, sizeof(poly)), poly[0] = 1; int dv = 1; for (int it : ex[x]) for (int j = 0; j < it; j++) mul(j), dv = dv * qpow(j + 1, M — 2) % M; int res = 0; for (int i = 0; i < MAXN; i++) { int cur = 0; for (int j = 0; j <= i; j++) cur += C[i + 1][j] * B[j] % M * qpow(lim + 1, i — j + 1) % M; cur %= M, cur = cur * qpow(i + 1, M — 2) % M; res = (res + cur * poly[i]) % M; } return res * dv % M;; }

void solve() { int n, m; cin >> n >> m; cout << m << ' '; for (int i = 2; i <= n; i++) cout << calc(i, m) << ' '; cout << '\n'; }

signed main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int T; cin >> T, init(), pwinit(); while (T--) solve(); }