В этой задаче проходило множество решений:
1) С каждым новым прямоугольником добавляется его площадь к результату, так что будем считать площадь каждого прямоугольника и прибавлять к ответу, т.е. для каждой строки x1, y1, x2, y2 прибавляем к ответу (x2 - x1 + 1) * (y2 - y1 + 1)
Асимптотика данного решения по времени O(n).
2) Просто сделаем все, что описано в условии, создадим массив и с каждым запросом будем прибавлять прямоугольник к массиву, после чего просто сложим все элементы массива.
Асимптотика по времени O(n * x * y)
Можно вывести формулу результата:
для n < 10 ответом будет n = n - 1 + 1 = 1 * (n + 1) - 1;
для n < 100 ответом будет 2 * (n - 9) + 9 = 2 * n - 9 = 2 * n - 10 - 1 + 2 = 2 * (n + 1) - 11;
для n < 1000 ответом будет 3 * (n - 99) + 2 * (99 - 9) + 9 = 3 * n - 99 - 9 = 3 * n - 100 - 10 - 1 + 3 = 3 * (n + 1) - 111;
для n < 10sz ответом будет 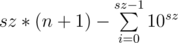 ;
;
Асимптотика по времени O(sz), где sz — длина числа.
Так же можно было просто перебрать всех возможных 10 вариантов n < 10, n < 100, ..., n < 109, n = 109 и подсчитывать для каждого результат.
UPD: Don't use function pow() to find powers of 10, because it doesn't work right sometimes.
Переведем число m в w-ичную систему счисления. Если все разряды числа – 0 или 1, то нашу вещь можно взвесить, поставив гири, номера разрядов которых равны 1, на одну чашу весов, а нашу вещь на другую.
Если же это условие не выполняется, то пройдемся от младшего разряда к старшему и если он не равен 0 или 1, пытаемся отнять от него w и прибавить к старшему разряду единицу. Если этот разряд становится равен - 1, то ставим гирю под данным номером на одну чашу с нашей вещью, если 0 — то не ставим гирю никуда, если иначе – то вещь нельзя взвесить по заданным условиям и ответ 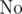 .
.
Асимптотика по времени O(logm).
Переберем все возможные пары точек, проведем через каждую из пар прямую и запишем, что этой прямой принадлежат эти 2 точки с помощью map. Если на прямой находится x точек, то на самом деле мы посчитаем нашим перебором, что на ней 2 * x * (x - 1) точек. Таким образом можно завести массив типа b[2 * x * (x - 1)] = x, чтобы определять, сколько точек находится на прямой. Тогда если на прямой находится x точек, то мы теряем x * (x - 1) * (x - 2) / 6 возможных треугольников с возможных n * (n - 1) * (n - 2) / 6 треугольников. Таким образом, для каждой прямой, на которой находится x точек, мы будем отнимать от n * (n - 1) * (n - 2) / 6 значение x * (x - 1) * (x - 2) / 6, таким образом подсчитывая ответ.
Асимптотика решения O(n2 * logn).
Поскольку map очень медленный, можно было для каждой пары точек каждую прямую заносить в массив, после этого отсортировать его и искать количество точек на каждой прямой нахождением количества подряд идущих одинаковых значений одной и той самой прямой.
UPD: I am sorry, that O(n3 / 6) solutions passed, my solution with O(n3 / 6) didn't pass before the contest, so I decided, that TL 4 sec is good(it was for Java TL).
Можно увидеть, что максимальный ответ будет тогда, когда скобки будут находится между двумя знаками * , или между знаком * и концом выражения. Для удобства прибавим в начало выражения 1 * , а в конец выражения * 1.
Далее переберем все возможные пары знаков * и попробуем посчитать выражение, поставив скобки между двумя знаками * для каждой пары.
Чтобы подсчитать выражение, используем две переменные x и y, в начале x = 0, y = firstnumber, где firstnumber — первая цифра выражения, тогда если следующий знак + , тогда x = y, y = nextnumber, а если * , тогда x = x, y = y * nextnumber. Результатом выражения будет x + y, для подсчета выражений в скобках и вне скобок можно написать функцию.
Асимптотика по времени O(|s| * 172).







