Adiv2

To solve the problem one could just store two arrays hused[j] and vused[j] sized n and filled with false initially. Then process intersections one by one from 1 to n, and if for i-th intersections both hused[h_i] and vused[v_i] are false, add i to answer and set both hused[h_i] and vused[v_i] with true meaning that h_i-th horizontal and v_i-th vertical roads are now asphalted, and skip asphalting the intersection roads otherwise.

Such solution has O(n²) complexity.

Bdiv2

It is always optimal to pass all the computers in the row, starting from 1-st to n-th, then from n-th to first, then again from first to n-th, etc. and collecting the information parts as possible, while not all of them are collected.

Such way gives robot maximal use of every direction change. O(n²) solution using this approach must have been passed system tests.

Adiv1

Let the answer be a₁ ≤ a₂ ≤ ... ≤ a_n. We will use the fact that gcd(a_i, a_j) ≤ a_min(i, j).

It is true that gcd(a_n, a_n) = a_n ≥ a_i ≥ gcd(a_i, a_j) for every 1 ≤ i, j ≤ n. That means that a_n is equal to maximum element in the table. Let set a_n to maximal element in the table and delete it from table elements set. We've deleted gcd(a_n, a_n), so the set now contains all gcd(a_i, a_j), for every 1 ≤ i, j ≤ n and 1 ≤ min(i, j) ≤ n - 1.

By the last two inequalities gcd(a_i, a_j) ≤ a_min(i, j) ≤ a_n - 1 = gcd(a_n - 1, a_n - 1). As soon as set contains gcd(a_n - 1, a_n - 1), the maximum element in current element set is equal to a_n - 1. As far as we already know a_n, let's delete the gcd(a_n - 1, a_n - 1), gcd(a_n - 1, a_n), gcd(a_n, a_n - 1) from the element set. Now set contains all the gcd(a_i, a_j), for every 1 ≤ i, j ≤ n and 1 ≤ min(i, j) ≤ n - 2.

We're repeating that operation for every k from n - 2 to 1, setting a_k to maximum element in the set and deleting the gcd(a_k, a_k), gcd(a_i, a_k), gcd(a_k, a_i) for every k < i ≤ n from the set.

One could prove correctness of this algorithm by mathematical induction. For performing deleting and getting maximum element operations one could use multiset or map structure, so solution has complexity .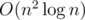

Bdiv1

There's an alternative solution. As soon as a₁, a₂, ..., a_nT contains maximum n distinct elements, it's any non-decreasing subsequence has a maximum of n - 1 increasing consequtive element pairs. Using that fact, one could calculate standard longest non-decreasing subsequence dynamic programming on first n array blocks (a₁, ..., a_n²) and longest non-decreasing subsequence DP on the last n array blocks (a_{nT - n + 1}, ..., a_nT). All other T - 2n blocks between them will make subsegment of consequtive equal elements in longest non-decreasing subsequence.

So, for fixed a_i, in which longest non-decreasing subsequence of length p on first n blocks array ends, and for fixed a_j ≥ a_i, in which longest non-decreasing subsequence of length s on last n blocks array starts, we must update the answer with p + (T - 2n)count(a_i) + s, where count(x) is the number of occurences of x in a₁, ..., a_n array. This gives us 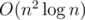solution.