To solve the problem one could just store two arrays hused[j] and vused[j] sized n and filled with false initially. Then process intersections one by one from 1 to n, and if for i-th intersections both hused[h_i] and vused[v_i] are false, add i to answer and set both hused[h_i] and vused[v_i] with true meaning that h_i-th horizontal and v_i-th vertical roads are now asphalted, and skip asphalting the intersection roads otherwise.

Such solution has O(n²) complexity.

Let the answer be a₁ ≤ a₂ ≤ ... ≤ a_n. We will use the fact that gcd(a_i, a_j) ≤ a_min(i, j).

It is true that gcd(a_n, a_n) = a_n ≥ a_i ≥ gcd(a_i, a_j) for every 1 ≤ i, j ≤ n. That means that a_n is equal to maximum element in the table. Let set a_n to maximal element in the table and delete it from table elements set. We've deleted gcd(a_n, a_n), so the set now contains all gcd(a_i, a_j), for every 1 ≤ i, j ≤ n and 1 ≤ min(i, j) ≤ n - 1.

By the last two inequalities gcd(a_i, a_j) ≤ a_min(i, j) ≤ a_n - 1 = gcd(a_n - 1, a_n - 1). As soon as set contains gcd(a_n - 1, a_n - 1), the maximum element in current element set is equal to a_n - 1. As far as we already know a_n, let's delete the gcd(a_n - 1, a_n - 1), gcd(a_n - 1, a_n), gcd(a_n, a_n - 1) from the element set. Now set contains all the gcd(a_i, a_j), for every 1 ≤ i, j ≤ n and 1 ≤ min(i, j) ≤ n - 2.

We're repeating that operation for every k from n - 2 to 1, setting a_k to maximum element in the set and deleting the gcd(a_k, a_k), gcd(a_i, a_k), gcd(a_k, a_i).

One could prove correctness of this algorithm by mathematical inductions. For performing deleting and getting maximum operations one could use multiset or map structure, so solution has complexity 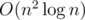.