Adiv2

To solve the problem one could just store two arrays hused[j] and vused[j] sized n and filled with false initially. Then process intersections one by one from 1 to n, and if for i-th intersections both hused[h_i] and vused[v_i] are false, add i to answer and set both hused[h_i] and vused[v_i] with true meaning that h_i-th horizontal and v_i-th vertical roads are now asphalted, and skip asphalting the intersection roads otherwise.

Such solution has O(n²) complexity.

Bdiv2

It is always optimal to pass all the computers in the row, starting from 1-st to n-th, then from n-th to first, then again from first to n-th, etc. and collecting the information parts as possible, while not all of them are collected.

Such way gives robot maximal use of every direction change. O(n²) solution using this approach must have been passed system tests.

Adiv1

Let the answer be a₁ ≤ a₂ ≤ ... ≤ a_n. We will use the fact that gcd(a_i, a_j) ≤ a_min(i, j).

It is true that gcd(a_n, a_n) = a_n ≥ a_i ≥ gcd(a_i, a_j) for every 1 ≤ i, j ≤ n. That means that a_n is equal to maximum element in the table. Let set a_n to maximal element in the table and delete it from table elements set. We've deleted gcd(a_n, a_n), so the set now contains all gcd(a_i, a_j), for every 1 ≤ i, j ≤ n and 1 ≤ min(i, j) ≤ n - 1.

By the last two inequalities gcd(a_i, a_j) ≤ a_min(i, j) ≤ a_n - 1 = gcd(a_n - 1, a_n - 1). As soon as set contains gcd(a_n - 1, a_n - 1), the maximum element in current element set is equal to a_n - 1. As far as we already know a_n, let's delete the gcd(a_n - 1, a_n - 1), gcd(a_n - 1, a_n), gcd(a_n, a_n - 1) from the element set. Now set contains all the gcd(a_i, a_j), for every 1 ≤ i, j ≤ n and 1 ≤ min(i, j) ≤ n - 2.

We're repeating that operation for every k from n - 2 to 1, setting a_k to maximum element in the set and deleting the gcd(a_k, a_k), gcd(a_i, a_k), gcd(a_k, a_i) for every k < i ≤ n from the set.

One could prove correctness of this algorithm by mathematical induction. For performing deleting and getting maximum element operations one could use multiset or map structure, so solution has complexity .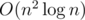

Bdiv1

One could calculate matrix sized n × n mt[i][j] — the length of the longest non-decreasing subsequence in array a₁, a₂, ..., a_n, starting at element, greater-or-equal to a_i and ending strictly in a_j element with j-th index.

One could prove that if we have two matrices sized n × n A[i][j] (the answer for a₁, a₂, ..., a_pn starting at element, greater-or-equal to a_i and ending strictly in a_j element with j-th index inside last block (a_{(p - 1)n + 1}, ..., a_pn) and B[i][j] (the answer for a₁, a₂, ..., a_qn \ldots), then the multiplication of this matrices in a way

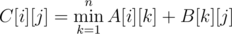
will give the same matrix but for length p + q. As soon as such multiplication is associative, next we will use fast matrix exponentiation algorithm to calculate M[i][j] (the answer for a₁, a₂, ..., a_nT) — matrix mt[i][j] raised in power T. The answer is the maximum in matrix M. Such solution has complexity .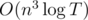

There's an alternative solution. As soon as a₁, a₂, ..., a_nT contains maximum n distinct elements, it's any non-decreasing subsequence has a maximum of n - 1 increasing consequtive element pairs. Using that fact, one could calculate standard longest non-decreasing subsequence dynamic programming on first n array blocks (a₁, ..., a_n²) and longest non-decreasing subsequence DP on the last n array blocks (a_{nT - n + 1}, ..., a_nT). All other T - 2n blocks between them will make subsegment of consequtive equal elements in longest non-decreasing subsequence.

So, for fixed a_i, in which longest non-decreasing subsequence of length p on first n blocks array ends, and for fixed a_j ≥ a_i, in which longest non-decreasing subsequence of length s on last n blocks array starts, we must update the answer with p + (T - 2n)count(a_i) + s, where count(x) is the number of occurences of x in a₁, ..., a_n array. This gives us solution.

Cdiv1

Let's fix s for every (l, s) pair. One could easily prove, that if subarray contains a_i element, than a_i must be greater-or-equal than a_j for every j such that i ≡ j ± od{gcd(n, s)}. Let's use this idea and fix g = gcd(n, s) (it must be a divisor of n). To check if a_i can be in subarray with such constraints, let's for every 0 ≤ r < g calculate

.

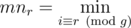It's true that every good subarray must consist of and only of 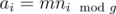. For finding all such subarrays we will use two pointers approach and for every good a_i, such that a_{(i - 1) ± od{n}} is not good we will find a_j such that a_i, a_{(i + 1) ± od{n}}, ... a_j are good and a_{(j + 1) ± od{n})} is not good. Let a_i, a_{(i + 1) ± od{n}}, ... a_j has k elements

Unable to parse markup [type=CF_TEX]

with count k, k - 1, ..., 1. As soon as sum of all k is not greater than n, we could just increase counts straightforward. There's a case when all a_i are good, in which we must do another increases. Next we must add to the answer only counts of length x, such that gcd(x, n) = g.

Solution described above has complexity O(d(n)n), where d(n) is the number of divisors of n.

Ddiv1

It is a common fact that for a prime p and integer n maximum α, such that p^α|n! is calculated as 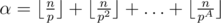, where p^A ≤ n < p^A + 1. As soon as , the maximum α for 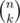is calculated as .

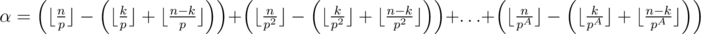One could see, that if we consider numbers n, k and n - k in p-th based numeric system, rounded-down division by p^x means dropping last x digits of its p-th based representation. As soon as k + (n - k) = n, every i-th summand in α corresponds to carry in adding k to n - k in p-th numeric system from i - 1-th to i-th digit position and is to be 0 or 1.

First, let convert A given in statement from 10 to p-th numeric system. In case, if α is greater than number of digits in A in p-th numeric system, the answer is 0. Next we will calculate dynamic programming on A p-th based representation.

dp[i][x][e][r] — the answer for prefix of length i possible equal to prefix of A representation (indicator e), x-th power of p was already calculated, and there must be carry equal to r from current to previous position. One could calculate it by bruteforcing all of p² variants of placing i-th digits in n and k according to r and e and i-th digit of A, and make a translation to next state. It can be avoided by noticing that the number of variants of placing digits is always a sum of arithmetic progression and can be calculated in O(1).

It's highly recommended to examine jury's solution with complexity O(|A|² + |A|min(|A|, α)).

Ediv1

One could prove that the number of binary functions on 4 variables is equal to 2²⁴, and can be coded by storing a 2⁴-bit binary mask, in which every bit is storing function value for corresponding variable set. It is true, that if mask_f and mask_g are correspond to functions f(A, B, C, D) and g(A, B, C, D), then function (f&g)(A, B, C, D) corresponds to

Unable to parse markup [type=CF_TEX]

bitmask. ()&() Now, we could parse expression given input into binary tree. I should notice that the number of nob-list nodes of such tree is not greater than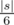 . Now, let's calculate dynamic programming on every vertex v — dp[v][mask] is the number of ways to place symbols in expression in the way that subtree of vertex v will correspond to function representing by mask. For list nodes such dynamic is calculated pretty straightforward by considering all possible mask values and matching it with the variable. One could easily recalculate it for one node using calculated answers for left and right subtree in 4¹⁶ operations: dp[v][lmask|rmask] +  = dp[l][lmask] * dp[r][rmask].

But all the task is how to make it faster. One could calculate s[mask], where s[mask] is equal to sum of all its submasks (the masks containing 1-bits only in positions where mask contains 1-bits) in 2⁴·2²⁴ operations using following code:

for (int mask = 0; mask < (1 << 16); ++mask) s[mask] = dp[x][mask];
for (int i = 0; i < 16; ++i)
    for (int mask = 0; mask < (1 << 16); ++mask)
        if (!(mask & (1 << i))) s[mask ^ (1 << i)] += s[mask];