Adiv2

Для решения задачи будем хранить два массива hused[j] и vused[j] размера n, изначально заполненных false. Будем обрабатывать перекрестки в списке от 1-го к n-му, и если для i-го перекрестка оба значения hused[h_i] и vused[v_i] равны false , i-ый день нужно добавить к ответу и установить значения hused[h_i] и vused[v_i] в true, означающих, что h_i-ая горизонтальная и v_i-ая вертикальная теперь заасфальтирована, а в противном случае нужно просто пропустить очередной перекресток.

Такое решение работает за O(n²).

Авторское решение: 13390628

Bdiv2

Чтобы получить оптимальный ответ, роботу нужно двигаться от первого компьютера к последнему, затем от последнего к первому, потом опять от первого к последнему, и т.д., попутно собирая те части информации, которые он может собрать на момент нахождения рядом с компьютером. Таким образом робот будет по максимуму использовать ресурсы, затраченные на смену направления движения. Несмотря на наличие более быстрых решений, от участников требовалось лишь решение с асимптотикой O(n²).

Авторское решение: 13390612

Adiv1

Пусть ответ представляет собой массив a₁ ≤ a₂ ≤ ... ≤ a_n. Далее будем пользоваться тем, что gcd(a_i, a_j) ≤ a_min(i, j).

Верно, что gcd(a_n, a_n) = a_n ≥ a_i ≥ gcd(a_i, a_j) для любых 1 ≤ i, j ≤ n. Это значит, что a_n равен максимальному элементу таблицы. Запишем в ответ a_n максимальный ответ и удалим его из текущего набора элементов. После удаления gcd(a_n, a_n) в наборе будут содержаться gcd(a_i, a_j) для любых 1 ≤ i, j ≤ n, таких, что 1 ≤ min(i, j) ≤ n - 1.

Из последних двух неравенств следует, что gcd(a_i, a_j) ≤ a_min(i, j) ≤ a_n - 1 = gcd(a_n - 1, a_n - 1). Поскольку в наборе содержится gcd(a_n - 1, a_n - 1), максимальный элемент в наборе равен a_n - 1. Поскольку a_n уже известен, удалим из набора gcd(a_n - 1, a_n - 1), gcd(a_n - 1, a_n), gcd(a_n, a_n - 1) . Теперь в наборе содержатся gcd(a_i, a_j), для любых 1 ≤ i, j ≤ n таких, что 1 ≤ min(i, j) ≤ n - 2.

Далее повторим это операцию для каждого k from n - 2 to 1, устанавливая a_k равным максимальному элементу в оставшемся наборе и удаляя gcd(a_k, a_k), gcd(a_i, a_k), gcd(a_k, a_i) для всех k < i ≤ n из набора.

С помощью математической индукции нетрудно доказать корректность такого алгоритма. Чтобы быстро выполнять удаление и получение максимального элемента в наборе, можно использовать, например, структуры map или set, что позволит реализовать решение с асимптотикой .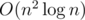

Авторское решение: 13390679

Bdiv1

Можно посчитать матрицу размера n × n mt[i][j] — длина наибольшей неубывающей подпоследовательности в массиве a₁, a₂, ..., a_n, начинающейся с элемента, не меньшего a_i и заканчивающейся непосредственно в элементе a_j.

Теперь, если мы имеем две матрицы размера n × n A[i][j] (ответ для массива a₁, a₂, ..., a_pn начинающегося с элемента, не меньшего a_i и заканчивающейся элементом a_j в последнем блоке массива (a_{(p - 1)n + 1}, ..., a_pn) и B[i][j] (ответ для массива a₁, a₂, ..., a_qn ), то произведение этих матриц

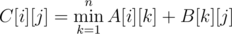
даст подобную матрицу, но для массива из p + q блоков. Так как такое произведение матриц является ассоциативным, воспользуемся быстрым возведением матрицы в степень для подсчета M[i][j] (ответ для массива a₁, a₂, ..., a_nT) — матрица mt[i][j] в степени T. Ответ на задачу — максимум матрицы M. Такое решение имеет асимптотику .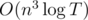

Авторское решение (с матрицами): 13390660

Существует альтернативное решение. Так как a₁, a₂, ..., a_nT содержит максимум n различных элементов, любая его неубывающая подпоследовательность содержит максимум n - 1 последовательных возрастающих соседних элементов. Пользуясь этим фактом, будем считать стандартное динамическое программирование на первых n блоках массива (a₁, ..., a_n²) и на n последних блоках массива (a_{nT - n + 1}, ..., a_nT). Все остальные блоки (а их T - 2n) между ними будут порождать равные элементы в результирующей неубывающей подпоследовательности.

Таким образом, для фиксированного a_i, в котором заканчивается неубывающая подпоследовательность длины p массива из первых n блоков, и для фиксированного a_j ≥ a_i, в котором аналогичная подпоследовательность длины s на последних n блоках массива начинается, нужно обновить ответ величиной p + (T - 2n)count(a_i) + s, где count(x) — количество вхождений x в массив a₁, ..., a_n. Получаем решение за .

Авторское решение ( с динамикой): 13390666

Cdiv1

Зафиксируем s и рассмотрим каждую пару (l, s). Тогда, если превосходящий подмассива содержит a_i, то a_i должен быть не меньше каждого a_j такого, что 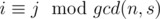. Будем использовать этот факт и решать задачу для фиксированного g = gcd(n, s) (g|n). Для последующей проверки того, что a_i может содержаться в превосходящем подмассиве, посчитаем для каждого 0 ≤ r < g

.

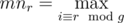Каждый периодический подмассив состоит из 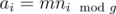и только из них. Для нахождения количества таких подмассивов будем пользоваться методом двух указателей и для каждого подходящего a_i такого, что 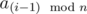не является подходящим, найдем такое a_j, что 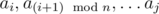являются подходящими и 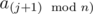не является подходящим. Пусть 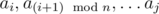представляет подотрезок из k элементов, т.е. 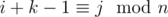. Любой подотрезок этого подотрезка так же является превосходящим, поэтому к отрезкам длины 1, 2, ..., k мы должны прибавить k, k - 1, ..., 1 соответственно. Так как сумма всех k не превосходит n, можно циклом увеличивать нужные значения. Случай, когда все a_i являются подходящими, нужно обрабатывать отдельно. После подсчета всех необходимых величин, мы должны добавить лишь те количества подотрезков длины x, для которых gcd(x, n) = g.

Описанное решение имеет асимптотику O(d(n)n), где d(n) — количество делителей n.

Авторское решение: 13390645

Ddiv1

Известно, что для простого p и натурального n максимальное α такое, что p^α|n!, вычисляется по формуле 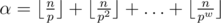, где p^w ≤ n < p^w + 1. Так как 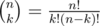, максимальное α для 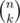вычисляется по формуле .

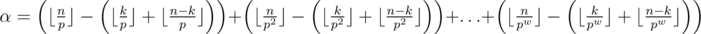Примечательно, что если представить n, k и n - k в p-ичной системе счисления, деление числа с округлением вниз на p^x соответствует отбрасыванию последних x цифр в его p-ичном представлении. Поскольку k + (n - k) = n, i-ое слагаемое в формуле для α соответствует величине переноса разряда с i - 1-ой к i-ой цифре в сложении k и n - k в p-ичной системе счисления и может принимать значения ноль или один.

Переведем A в p-ичную систему счисления и будем далее работать только с этим его представлением. В случае, если α превышает количество цифр в представлении A то, как описано выше, ответ равен 0. Далее будем считать динамическое программирование на представлении числа A.

dp[i][x][e][r] — ответ, если мы рассмотрели первые i цифр числа n и k, при этом эти цифры в n могут равняться первым цифрам A (булева e), x-ая степень p уже была набрана, и величина переноса с текущего в следующий разряд равна r . Переходы будем осуществлять вперед, имея, таким образом, не более p² вариантов расстановки цифр в n и k. Поскольку перебор всех таких вариантов невозможен, нужно заметить, что для перехода в фиксированное состояние (его первый параметр равен i + 1) количество вариантов расстановки цифр равняется сумме арифметической прогрессии, поэтому переход с помощью умножения на сумму прогрессии можно осуществлять за O(1).

Крайне рекомендуется ознакомиться с авторским решением за O(|A|² + |A|min(|A|, α)).

Авторское решение: 13390698

Ediv1

One could prove that the number of binary functions on 4 variables is equal to 2²⁴, and can be coded by storing a 2⁴-bit binary mask, in which every bit is storing function value for corresponding variable set. It is true, that if mask_f and mask_g are correspond to functions f(A, B, C, D) and g(A, B, C, D), then function (f&g)(A, B, C, D) corresponds to mask_f&mask_g bitmask.

Now, we could parse expression given input into binary tree. I should notice that the number of non-list nodes of such tree is about 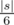. Now, let's calculate dynamic programming on every vertex v — dp[v][mask] is the number of ways to place symbols in expression in the way that subtree of vertex v will correspond to function representing by mask. For list nodes such dynamic is calculated pretty straightforward by considering all possible mask values and matching it with the variable. One could easily recalculate it for one node using calculated answers for left and right subtree in 4¹⁶ operations: dp[v][lmask|rmask] +  = dp[l][lmask] * dp[r][rmask].

But all the task is how to make it faster. One could calculate s[mask], where s[mask] is equal to sum of all its submasks (the masks containing 1-bits only in positions where mask contains 1-bits) in 2⁴·2²⁴ operations using following code:

for (int mask = 0; mask < (1 << 16); ++mask) s[mask] = dp[x][mask];
for (int i = 0; i < 16; ++i)
    for (int mask = 0; mask < (1 << 16); ++mask)
        if (!(mask & (1 << i))) s[mask ^ (1 << i)] += s[mask];

Let's calculate sl[mask] and sr[mask] for dp[l][mask] and dp[r][mask] respectively. If we will find s[mask] = sl[mask] * sr[mask], s[mask] will contain multiplications of values of pairs of masks from left and right dp's, which are submasks of mask. As soon as we need pairs, which in bitwise OR will give us exactly mask, we should exclude pairs, which in bitwise OR gives a submask of mask, not equal to mask. This gives us exclusion-inclusion principle idea. The formula of this will be

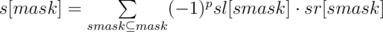, where p is the parity of number of bits in mask^submask.

Such sum could be calculated with approach above, but subtracting instead of adding

for (int mask = 0; mask < (1 << 16); ++mask) s[mask] = sl[mask] * sr[mask];
for (int i = 0; i < 16; ++i)
    for (int mask = 0; mask < (1 << 16); ++mask)
        if (!(mask & (1 << i))) s[mask ^ (1 << i)] -= s[mask];

In such way we will recalculate dynamic for one vertex in about 3·2⁴·2¹⁶ operations.

Jury's solution: 13390713