Оптимально делать наибольший возможный шаг каждый раз. Поэтому слоник должен сделать сначала некоторое количество шагов на расстояние 5, а затем один или ноль шагов на меньшее расстояние. Следовательно, ответ равен 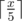 .
.
Нам дан массив, состоящий только из нулей и единиц. Мы должны разделить его на части, в каждой из которых ровно одна единица.
Особый случай: когда массив состоит только из нулей ответ равен нулю.
Рассмотрим общий случай. Во-первых нули на префиксе относятся к первому куску, нули на суффиксе относятся ко второму куску. Во-вторых, между каждой парой соседних единиц должно быть одно и только одно разделение частей. Между соседними единицами с индексами a < b всего b - a вариантов разделения. Поэтому мы должны перемножить эти значения для всех пар соседних единиц.
Бонус: каким является максимальный ответ при n ≤ 100?
Первый радиус равен нулю или расстоянию от первого фонтана до какого-то цветка. Переберем все эти числа. Второй радиус будет равен максимальному из расстояний от второго фонтана до цветка, который не принадлежит кругу с первым радиусом. Теперь мы должны выбрать вариант с минимальным r12 + r22
Бонус: Я описал решение за O(n2). Можете ли вы решить задачу за O(nlogn)?
Ответ равен одному, когда все координаты x или все координаты y совпадают.
Когда ответ равен двум? Переберем все пары точек. Пусть первая точка является началом ломаной, вторая концом ломаной. Только одна или две таких ломаных с двумя звеньями существуют. Они образуют прямоугольник с противоположными углами в первой и второй точке. Мы можем просто проверить принадлежность третьей точки прямоугольнику.
Иначе ответ всегда равен трем. Давайте построим вертикальные прямые через самую левую и через самую правую точки. Через третью точку построим горизонтальную прямую. Теперь, если мы удалим некоторые лишние лучи, получим подходящую ломаную.
617E - XOR and Favorite Number
У нас есть массив a
Давайте посчитаем массив 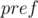 (
(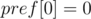 ,
, 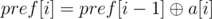 ).
).
Xor подмассива 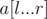 равен
равен 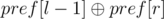 .
.
Теперь запрос (l, r) заключается в подсчете количества пар i, j (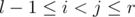 )
) 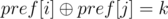 .
.
Пусть мы знаем ответ на запрос (l, r) и знаем для всех v cnt[v] — количество вхождений v в 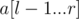 .
.
Мы можем обновить за O(1) ответ и cnt если мы изменим правую или левую границу запроса на 1.
Поэтому мы можем решить задачу оффлайн за 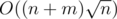 с помощью корневой эвристики (алгоритм Мо).
с помощью корневой эвристики (алгоритм Мо).






