Aim — To multiply 2 n-degree polynomials in 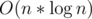 instead of the trivial O(n2)
instead of the trivial O(n2)
I have poked around a lot of resources to understand FFT (fast fourier transform), but the math behind it would intimidate me and I would never really try to learn it. Finally last week I learned it from some pdfs and CLRS by building up an intuition of what is actually happening in the algorithm. Using this article I intend to clarify the concept to myself and bring all that I read under one article which would be simple to understand for others struggling with fft.
Let’s get started 
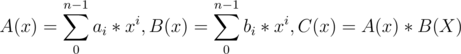
Here A(x) and B(x) are polynomials of degree n - 1. Now we want to retrieve C(x) in 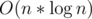
So our methodology would be this 
- Convert A(x) and B(x) from coefficient form to point value form. (FFT)
- Now do the O(n) convulsion in point value form to obtain C(x) in point value form, i.e. basically C(x) = A(x) * B(x) in point value form.
- Now convert C(x) from point value from to coefficient form (Inverse FFT).
Well, a polynomial A(x) of degree n can be represented in its point value form like this  A(x) = {(x0, y0), (x1, y1), (x2, y2), ..., (xn - 1, yn - 1)} , where yk = A(xk) and all the xk are distinct.
A(x) = {(x0, y0), (x1, y1), (x2, y2), ..., (xn - 1, yn - 1)} , where yk = A(xk) and all the xk are distinct.
So basically the first element of the pair is the value of x for which we computed the function and second value in the pair is the value which is computed i.e A(xk).
Also the point value form and coefficient form has one-to-one correspondence i.e. for each point value form there is exactly one coefficient representation and vice — versa, If for k degree polynomial, k + 1 point value forms have been used at least.
Reason is simple, the point value form has n variables i.e, a0, a1, ..., an - 1 and n equations i.e. y0 = A(x0), y1 = A(x1), ..., yn - 1 = A(xn - 1) so only one solution is there.
Now using matrix multiplication the conversion from coefficient form to point value form for the polynomial 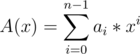 can be shown like this
can be shown like this 
And the inverse, that is the conversion from point value form to coefficient form for the same polynomial can be shown as this 
Note —
A(x) = {(1, 5), (2, 3), (3, 2)} and B(x) = {(1, 3), (2, 4), (3, 7)}, where degree of A(x) and B(x) = 2
Now as C(x) = A(x) * B(x)
C(1) = A(1) * B(1) = 5 * 3 = 15, C(2) = A(2) * B(2) = 3 * 4 = 12, C(3) = A(3) * B(3) = 2 * 7 = 14
So C(x) = {(1, 15), (2, 12), (3, 14)} where degree of C(x) = degree of A(x) + degree of B(x) = 4 But we know that a polynomial of degree n-1requires n point value pairs, so 3 pairs of C(x)are not sufficient for determining C(x) uniquely as it is a polynomial of degree 4. Therefore we need to calculate A(x) and B(x), for 2npoint value pairs instead of n point value pairs so that C(x)’s point value form contains 2npairs which would be sufficient to uniquely determine C(x) which would have a degree of 2(n — 1).






