Aim — To multiply 2 n-degree polynomials in 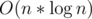instead of the trivial O(n²)

I have poked around a lot of resources to understand FFT (fast fourier transform), but the math behind it would intimidate me and I would never really try to learn it. Finally last week I learned it from some pdfs and CLRS by building up an intuition of what is actually happening in the algorithm. Using this article I intend to clarify the concept to myself and bring all that I read under one article which would be simple to understand for others struggling with fft.

Let’s get started

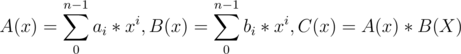
Here A(x) and B(x) are polynomials of degree n - 1. Now we want to retrieve C(x) in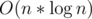

So our methodology would be this

1. Convert A(x) and B(x) from coefficient form to point value form. (FFT)
2. Now do the O(n) convulsion in point value form to obtain C(x) in point value form, i.e. basically C(x) = A(x) * B(x) in point value form.
3. Now convert C(x) from point value from to coefficient form (Inverse FFT).

Q) What is point value form ?
Ans) Well, a polynomial A(x) of degree n can be represented in its point value form like this A(x) = {(x₀, y₀), (x₁, y₁), (x₂, y₂), ..., (x_n - 1, y_n - 1)} , where y_k = A(x_k) and all the x_k are distinct.
So basically the first element of the pair is the value of x for which we computed the function and second value in the pair is the value which is computed i.e A(x_k).
Also the point value form and coefficient form has one-to-one correspondence i.e. for each point value form there is exactly one coefficient representation and vice — versa, If for k degree polynomial, k + 1 point value forms have been used at least.
Reason is simple, the point value form has n variables i.e, a₀, a₁, ..., a_n - 1 and n equations i.e. y₀ = A(x₀), y₁ = A(x₁), ..., y_n - 1 = A(x_n - 1) so only one solution is there.
Now using matrix multiplication the conversion from coefficient form to point value form for the polynomial 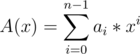can be shown like this
And the inverse, that is the conversion from point value form to coefficient form for the same polynomial can be shown as this

Note —
A(x) = {(1, 5), (2, 3), (3, 2)} and B(x) = {(1, 3), (2, 4), (3, 7)}, where degree of A(x) and B(x) = 2
Now as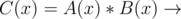

C(1) = A(1) * B(1) = 5 * 3 = 15, C(2) = A(2) * B(2) = 3 * 4 = 12, C(3) = A(3) * B(3) = 2 * 7 = 14

So C(x) = {(1, 15), (2, 12), (3, 14)} where degree of C(x) = degree of A(x) + degree of B(x) = 4
But we know that a polynomial of degree n - 1 requires n point value pairs, so 3 pairs of C(x) are not sufficient for determining C(x) uniquely as it is a polynomial of degree 4.
Therefore we need to calculate A(x) and B(x), for 2n point value pairs instead of n point value pairs so that C(x)’s point value form contains 2n pairs which would be sufficient to uniquely determine C(x) which would have a degree of 2(n - 1).

Now if we had performed this algorithm naively it would have gone on like this

Note — This is NOT the actual FFT algorithm but I would say that understanding this would layout framework to the real thing.
Note — This is actually DFT algorithm, ie. Discrete fourier transform.

1. We construct the point value form of A(x) and B(x) using x₀, x₁, ..., x_2n - 1 which can be made using random distinct integers. So point value form of A(x) = {(x₀, 0), (x₁, 1), (x₂, 2), ..., (x_2n - 1, 2n - 1)} and B(x) = {(x0, 0), (x1, 1), (x2, 2), ..., (x2n - 1, 2n - 1)} Note — The x₀, x₁, ..., x_2n - 1 should be same for $A(x) and $B(x). This conversion takes O(n²).
2. As C(x) = A(x) * B(x), then what would have been the point-value form of C(x) ?
   If we plug in x₀ to all 3 equations then we see that
   C(x₀) = A(x₀) * B(x₀)
   C(x₀) = 0 * 0
   So C(x) in point value form will be C(x) = {(x₀, 0 * 0), (x₁, 1 * 1), (x₂, 2 * 2), ..., (x_2n - 1, 2n - 1 * 2n - 1)}
   This is the convulsion, and it’s time complexity is O(n)
3. Now converting C(x) back from point value form to coefficient form can be represented by using the equation 2. Here calculating the inverse of the matrix requires LU decomposition or Lagrange’s Formula. I won’t be going into depth on how to do the inverse, and am just giving this link, to anyone who is interested to read about it. But we get to understand that using Lagrange’s Formula we would’ve been able to do this step in O(n²).

Note — Here the algorithm was performed wherein we used x₀, x₁, ..., x_2n - 1 as ordinary real numbers, the FFT on the other hand uses roots of unity instead and we are able to optimize the O(n²) conversions from coefficient to point value form and vice versa to 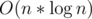because of the special mathematical properties of roots of unity which allows us to use the divide and conquer approach. I would recommend to stop here and re-read the article till here until the algorithm is crystal clear as this is the raw concept of FFT.