660A - Взаимнопростый массив
Задача предложена пользователем Ali Ibrahim C137.
Заметим, что если есть пара соседних не взаимнопростых чисел, то мы обязаны между ними вставить какое-нибудь число. С другой стороны мы всегда можем вставить число 1.
Сложность: O(nlogn).
660B - Рассадка в автобусе
Задача предложена пользователем Srikanth Bhat bharsi.
В этой задаче нужно было сделать ровно то, что написано в условии. Никаких хитростей и подвохов.
Сложность: O(n).
660C - Сложный процесс
Задача предложена пользователем Mohammad Amin Raeisi Smaug.
Назовём отрезок [l, r] хорошим если в нём не более k ноликов. Заметим, что если отрезок [l, r] хороший, то отрезок [l + 1, r] тоже хороший. Таким образом, можно воспользоваться методом двух указателей: один указатель это l, а второй это r. Будем перебирать l слева направо и двигать r пока можем (для этого нужно просто поддерживать количество ноликов в текущем отрезке).
Сложность: O(n + k).
660D - Количество параллелограммов
Задачу предложена участником Sadegh Mahdavi smahdavi4.
Как известно диагонали параллелограмма делят друг друга пополам. Переберём пару точек a, b и рассмотрим середину отрезка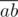 
: c = (a + b) / 2. Для всех середин отрезков посчитаем число cntc — количество пар точек, с этой серединой. Легко видеть, что ответ это 
.
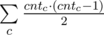Сложность: O(n2logn).
652E - В погоне за артефактами
Задача предложена пользователем Lewin Gan Lewin.
Рассмотрим некоторую подпоследовательность длины k > 0 (пустые подпоследовательности можно учесть отдельно, прибавив в конце к ответу число mn) и посчитаем количество последовательностей в которых она будет учтена. Нам это нужно сделать аккуратно, чтобы всё посчитать ровно по одному разу. Пусть x1, x2, ... , xk это наша подпоследовательность. Тогда в исходной последовательности перед элементом x1 могли находиться ещё числа, но число x1 не могло встретиться (поскольку мы хотим всё посчитать по разу, варианты когда x1 уже встречалось нам не нужно учитывать). Таким образом, у нас (m - 1) вариант для каждого из чисел перед x1. Аналогичо, между числами x1 и x2 могут находиться некоторые числа (но не может находиться число x2). И так далее. После числа xk может находиться ещё некоторое количество чисел (пусть их j штук), причём на них не накладывается никаких ограничений (то есть m вариантов для каждого числа). Мы зафиксировали, что в конце стоит j чисел, значит n - k - j чисел нужно распределить между числами перед x1, между x1 и x2, \ldots , между xk - 1 и xk. Легко видеть, что это можно сделать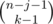 
способами (это просто биномиальный коэффициент с повторениями). Количество последовательностей x1, x2, ... , xk, конечно, равно mk. Таким образом, ответ это 
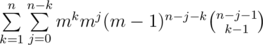. Последнюю сумму легко преобразовать к виду 
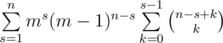. Заметим, что последняя внутренняя сумма легко суммируется с помощью известной формулы параллельного суммирования: 
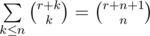. Таким образом, ответ равен: 
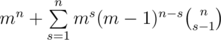. Можно далее сворачивать сумму, чтобы получить логарифмическое решение (закнутую формулу), но в задаче это не требовалось.
Сложность: O((n + m)log MOD), где MOD = 109 + 7.
