I recently implemented Treap, one of various kinds of binary search trees (BSTs), on Rust. It is a balanced BST, which means that it ensures that tree depth is always 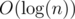where n =  (the number of items in a tree). That is achieved by using randomisation. (For more details see Treap — Wikipedia.)

Here are results of some experiments:

(1) Insertion of 10000 elements in the ascending order:
http://ideone.com/tSrw7u
It took 11.7 seconds to insert 30000 elements in the ascending order, and it got Time Limit Exceeded (>15.0sec) when the number of elements is >100000. You'll see that the depth of the treap increases in logarithmic speed.

(2) Insertion of 10000 elements in a random order:
http://ideone.com/yxVe6d
It took 11.8 seconds to insert 30000 elements in a random order. Like (1), the depth of the treap increases in logarithmic speed, too.

Here is a graph that indicates how the depth of the treap grows as the number of elements increases.

Iikanjino Gurafu

The code I used in this experiment is avaliable at: https://github.com/koba-e964/contest/blob/906fcb07057b72496407b3c6e6a422e48e60dc6f/comm/Treap.rs