Me and my teammate maverick16 were doing the Problem I.Critical Structures, in this Problem set and this is the CF Problem page.
In this problem, we are given a connected graph G and the following terminologies are defined:- 1. Critical node: a node in G whose removal disconnects G. 2. Critical link: an edge in G whose removal disconnects G. 3. Critical component: a maximal set of edges in G such that any two edges in the set lie on a common cycle (A cycle is a set of nodes ⟨v0, v1, . . . , v k−1 ⟩, where k ≥ 4, such that any two consecutive vi−1 and vi for 1 ≤ i ≤ k − 1 have an edge, v0 = vk−1 and vi for 0 ≤ i ≤ k −2 are all distinct. 4. Largest critical component: a critical component with the maximum number of edges.
We are asked to find the number of critical nodes, critical link, p and q, where p/q is of irreducible form and p and q are defined as:- - p is the number of critical components in the graph - q is the number of edges in the largest critical component
Our approach to this problem is :
find all the bridges and cut vertices first, remove all the bridges. now apply dfs through individual component and count the edges in that component, we divided this into two cases from here:-
- there a single cut vertex in the component remove it and count both components (components separated by cut vertex) as different
- else take the complete component as a single critical component
p will be the number of components counted with this dfs + bridges and q will be max edges in a component.
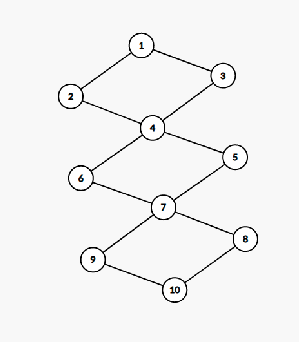
But, this approach should fail, when the graph looks like this, however it passed all tests, can anyone help with this?