Hello, Codeforces!
A few days ago MohammadParsaElahimanesh posted a blog titled Can we find each Required node in segment tree in O(1)? Apparently what they meant was to find each node in $$$\mathcal{O}(ans)$$$, according to ecnerwala's explanation. But I was too dumb to realize that and accidentally invented a parallel node resolution method instead, which speeds up segment tree a lot.
A benchmark for you first, with 30 million RMQ on a 32-bit integer array of 17 million elements. It was run in custom test on Codeforces on Apr 6, 2021.
- Classic implementation from cp-algorithms: 7.765 seconds, or 260 ns per query
- Optimized classic implementation: (which I was taught) 4.452 seconds, or 150 ns per query (75% faster than classic)
- Bottom-up implementation: 1.914 seconds, or 64 ns per query (133% faster than optimized)
- Novel parallel implementation: 0.383 seconds, or 13 ns per query (400% faster than bottom-up, or 2000% faster than classic implementation)
FAQ
Q: Is it really that fast? I shamelessly stole someone's solution for 1355C - Сосчитайте треугольники which uses prefix sums: 112167743. It runs in 46 ms. Then I replaced prefix sums with classic segment tree in 112168469 which runs in 155 ms. The bottom-up implementation runs in 93 ms: 112168530. Finally, my novel implementation runs in only 62 ms: 112168574. Compared to the original prefix sums solution, the bottom-up segment tree uses 47 ms in total, and the parallel implementation uses only 16 ms in total. Thus, even in such a simple problem with only prefix queries the novel implementation is 3x faster than the state of art even in practice!
Q: Why? Maybe you want your $$$\mathcal{O}(n \log^2 n)$$$ solution to pass in a problem with $$$\mathcal{O}(n \log n)$$$ model solution. Maybe you want to troll problemsetters. Maybe you want to obfuscate your code so that no one would understand you used a segment tree so that no one hacks you (just kidding, you'll get FST anyway). Choose an excuse for yourself. I want contribution too.
Q: License? Tough question because we're in CP. So you may use it under MIT license for competitive programming, e.g. on Codeforces, and under GPLv3 otherwise.
Q: Any pitfalls? Yes, sadly. It requires AVX2 instructions which are supported on Codeforces, but may not be supported on other judges.
How it works
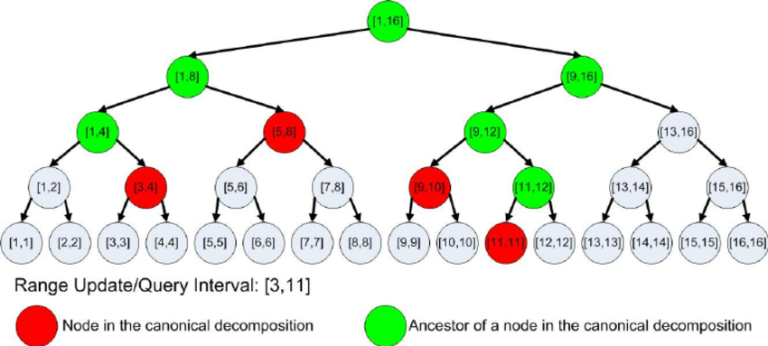
In a segment tree, a range query is decomposed into red nodes. Classic segment tree implementations don't find these red nodes directly, but execute recursively on green nodes. Bottom-up segment tree implementation does enumerate these nodes directly, but it also enumerates a few other unused nodes.
The parallel implementation is an optimization of bottom-up tree. Probably you all know how bottom-up implementation looks like, but I'll cite the main idea nevertheless to show the difference between bottom-up and parallel implementations:
In bottom-up segment tree, we find the node corresponding to the leftmost element of the query, i.e. $$$x[l]$$$, and the node corresponding to the rightmost query element, i.e. $$$x[r]$$$. If we numerate nodes in a special way, the leftmost element will correspond to node $$$N+l$$$ and the rightmost will correspond to node $$$N+r$$$. After that, the answer is simply the sum of values of all nodes between
Unable to parse markup [type=CF_MATHJAX]
. Sadly there are $$$\mathcal{O}(n)$$$ of those, but we can do the following optimization:If $$$N+l$$$ is the left child of its parent and $$$N+r$$$ is the right child of its parent, then instead of summing up all nodes in range $$$[N+l, N+r]$$$, we can sum up all nodes in range $$$[\frac{N+l}{2}, \frac{N+r-1}{2}]$$$. That is, we replace the two nodes with their two parents. Otherwise, if $$$N+l$$$ is the right child of its parent, we do ans += a[N+l]; l++;, and if $$$N+r$$$ is the left child of its parent, we do ans += a[N+r]; r--; Then the condition holds and we can do the replacement.
In parallel segment tree, we jump to i-th parent of $$$N+l$$$ and $$$N+r$$$ for all $$$i$$$ simultaneously, and check the is-left/right-child conditions in parallel as well. The checks are rather simple, so a few bit operations do the trick. We can perform all bitwise operations using AVX2 on 8 integers at once, which means that the core of the query should run about 8 times faster.
Want code? We have some!
This is the benchmark, along with the four segment tree implementations I checked and a prefix sum for comparison.






