NAIPC is coming up on April 15 (start time here). More information can be found on the site. The contest will be on Kattis on the 15th. About 15 hours later, it will be available as an open cup round as the Grand Prix of America. Please only participate in one of them, and don't discuss problems here until after the open cup round.

The deadline to register for the contest on Kattis is April 12th. You can register by following instructions on this site: http://naipc.uchicago.edu/2017/registration.html# You will need an ICPC account to register.

You can see previous NAIPC rounds here: 2015, 2016. 2016 is also available in the codeforces gym here: http://codeforces.net/gym/101002

UPD 1: The deadline to register is in a couple of days.

UPD 2: Both contests are now over

NAIPC standings: https://naipc17.kattis.com/standings

Open Cup standings: http://opentrains.snarknews.info/~ejudge/res/res10376

I'll update this one more time with solutions once they are up.

UPD 3: Test data is available here (solutions may show up later, but I'm not sure when): http://serjudging.vanb.org/?p=1050

Hello everyone!

I’d like you to invite for CodeChef March Cook-Off that will start at 21:30 IST of 19-th March 2017 (check your time zone here) and will last 2.5 hours.

I am the author of problems and editorials, while Errichto is the tester. There are also some other people who helped with translations and miscellaneous issues who I will fill in later.

There is no registration required, anybody with a CodeChef handle can participate. Top participants can win CodeChef laddus (details on the contest page).

You will be provided 5 problems. There's one problem that shows a style of problems I would like to see more in competitions. Let me know what your thoughts are after the contest.

Hope to see you all on the leaderboard!

I recently added this regional to the gym. I set it to start at this time, but I think you can just do virtual participation whenever you want.

I set about 5 of the problems on the set. I would say difficulty goes up to around div1D.

Solutions are available on the contest website if you want to look those up afterwards. Let me know what you think of the problems afterwards!

Short solutions:

• Div2A: How many times do we need to do a cyclic shift to consider all possible ones? Afterwards, what data structure allows us to easily check number of distinct elements?
• Div2B: Imagine the process in reverse. What types of identical shapes can I get if I cut a rectangle into two pieces? Remember, pieces cannot be rotated or flipped.
• Div2C / Div1A: How do we handle components with special nodes? What do we do with the ones without special nodes?
• Div2D / Div1B: We don't get many questions, so is there a way to "parallelize" questions? Another approach, can we split up the condition i != j somehow using bits?
• Div2E / Div1C: First, somehow reduce it so r_i,b_i <= n. Now, we can bound the excess tokens by a small number, so we can do bitmask dp from here.
• Div1D: The optimal circle must touch a blue point. Now, either consider the inversion, or do a binary search
• Div1E: What makes a list good? How fast can we do this check, and how many times do we need to do this check?

Long solutions:

Hongcow Learns the Cyclic Shift

We only need to consider at most |s| cyclic shifts (since |s| cyclic shifts returns us back to the original string).

So, we can put these all in a set, and return the size of the set.

print (lambda s: len(set(s[i:] + s[:i] for i in range(len(s)))))(raw_input())

Hongcow Solves A Puzzle

I really apologize for the ambiguity of this problem. We worked hard to make it concise and accurate, but we left out too many details.

Basically, the idea is we want to overlay two of these pieces together so that no square has more than 1 X, and the region of X's forms a rectangle.

Now for the solution:

First, let's look at it backwards. I have a rectangle, and I cut it in two pieces. These two pieces have the same exact shape. What shapes can I form?

A necessary and sufficient condition is that the piece itself is a rectangle itself! There are a few ways to check this. One is, find the min/max x/y coordinates, and make sure the number of X's match the bounding box of all the points.

n,m = map(int, raw_input().split())
piece = [raw_input().rstrip() for i in range(n)]

maxx, minx, maxy, miny = -1, n, -1, m
count = 0
for i in range(n):
	for j in range(m):
		if piece[i][j] == 'X':
			maxx = max(maxx, i)
			minx = min(minx, i)
			maxy = max(maxy, j)
			miny = min(miny, j)
			count += 1


print ((maxx - minx + 1) * (maxy - miny + 1) == count) * "YES" or "NO"

Hongcow Builds a Nation

First, let's make all connected components cliques. This graph is still stable.

Now, there are some components without special nodes. Where should we connect them?

If there is a component with size A and a component with size B, we can add A*B edges if we connect these two components. So, it makes sense to choose the largest component.

n,m,k = map(int, raw_input().split())
special = map(int, raw_input().split())

root = range(n+1)

def par(p):
	if p != root[p]:
		root[p] = par(root[p])
	return root[p]

def c2(n):
	return n * (n - 1) / 2

for __ in xrange(m):
	u,v = map(par, map(int, raw_input().split()))
	root[v] = u

sz = [0 for i in range(n+1)]
for i in range(n+1):
	sz[par(i)] += 1

leftover = n
ans = 0
largest = 0
for x in special:
	d = par(x)
	largest = max(largest, sz[d])
	ans += c2(sz[d])
	leftover -= sz[d]

ans -= c2(largest)
ans += c2(largest + leftover)
ans -= m

print ans

Hongcow's Game

For the bits solution: We want to create 20 questions where for every i != j, there exists a question

that contains j and not i, and also a qusetion that contains i and not j. If we can do this, we can find the min for each row.

Note that i != j implies that there exists a bit index where i and j differ.

So, let's ask 2 questions for each bit position, one where all indices have a value of 0 in that position, and one where all indices have a value of 1 in that position. This is a total of at most 20 questions, and we can show that this satisfies the condition above, so this solves the problem.

Parallelization will basically reduce to the above solution, but is another way of looking at the problem.

First, let's ask {1,2,...,n/2} and {n/2+1,...,n} This handles the case where the min lies on the opposite half.

[
OOOOXXXX
OOOOXXXX
OOOOXXXX
OOOOXXXX
XXXXOOOO
XXXXOOOO
XXXXOOOO
XXXXOOOO
]

For example, this handles the case where the min lies in the X part of the matrix, and we split it into two identical problems of size n/2 within the O matrix.

Now, we can ask questions for each submatrix, but we can notice that these two don't interact so we can combine all the questions at this level.

However, we should ask the questions in parallel, as we don't have that many questions For example, for n=8, we should ask

First level:
[1,2,3,4]
[5,6,7,8]

Second level
[1,2],[5,6] (i.e. ask 1,2,5,6 all together, but this is actually two different subproblems, one for the top left, and one for the bottom right).
[3,4],[7,8]

Third level
[1],[3],[5],[7]
[2],[4],[6],[8]

As you can see, this reduces to the bit approach above if N is a power of 2.

import java.io.PrintWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

public class HiddenMatrix {
    public static void main (String[] args) {
        Scanner in = new Scanner(System.in);
        PrintWriter out = new PrintWriter(System.out);
        int n = in.nextInt();
        int[] min = new int[n+1];
        Arrays.fill(min, 1 << 30);
        for (int bit = 0; bit < 10; bit++) {
            for (int val = 0; val <= 1; val++) {
                ArrayList<Integer> query = new ArrayList<>();
                for (int i = 1; i <= n; i++) {
                    if (((i >> bit) & 1) == val) {
                        query.add(i);
                    }
                }
                if (query.size() != n && query.size() != 0) {
                    out.println(query.size());
                    for (int j = 0; j < query.size(); j++) {
                        if (j != 0) out.print(" ");
                        out.print(query.get(j));
                    }
                    out.println();
                    out.flush();

                    for (int i = 1; i <= n; i++) {
                        int d = in.nextInt();
                        if (((i >> bit) & 1) == 1 - val) {
                            min[i] = Math.min(min[i], d);
                        }
                    }
                }
            }
        }

        out.println(-1);
        for (int i = 1; i <= n; i++) {
            if (i != 1) out.print(" ");
            out.print(min[i]);
        }
        out.println();
        out.flush();
        System.exit(0);
    }
}

Hongcow Buys a Deck of Cards

Also note that if r_i or b_i >= n, we need to collect tokens no matter what since those costs can't be offset. So, we can assume that r_i, b_i <= n.

Let's only buy tokens when we need them. Note that after buying a card, you will have either 0 red tokens or 0 blue tokens, so our dp state can be described by [mask][which one is zero][how many of the other] The dimensions of this dp table are 2^n * 2 * (n^2) (n^2 because the costs to buy cards is at most n).

See the code for more details on how to update this dp.

import java.util.Arrays;
import java.util.Scanner;

public class RedAndBlueCards {
    public static int n;
    public static char[] color;
    public static int[] r,b;
    public static int[] countred, countblue;
    public static void main (String[] args) {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        color = new char[n];
        r = new int[n];
        b = new int[n];
        int base = 0;
        int needred = 0, needblue = 0;
        for (int i = 0; i < n; i++) {
            color[i] = in.next().charAt(0);
            r[i] = in.nextInt();
            b[i] = in.nextInt();
            needred += Math.max(0, r[i] - n);
            needblue += Math.max(0, b[i] - n);
            r[i] = Math.min(n, r[i]);
            b[i] = Math.min(n, b[i]);
        }
        base = Math.max(needred, needblue);

        countred = new int[1<<n];
        countblue = new int[1<<n];
        for (int i = 1; i < 1 << n; i++) {
            int lowbit = Integer.numberOfTrailingZeros(i & -i);
            countred[i] = countred[i ^ (1 << lowbit)];
            countblue[i] = countblue[i ^ (1 << lowbit)];
            if (color[lowbit] == 'R') countred[i]++;
            else countblue[i]++;
        }

        dp = new int[2][n*n+1][1<<n];
        for (int[][] x : dp) for (int[] y : x) Arrays.fill(y, -1);

        int ans = base + n;
        if (needred < needblue) {
            ans += solve(0, 0, needblue - needred);
        } else {
            ans += solve(0, 1, needred - needblue);
        }
        System.out.println(ans);
        System.exit(0);
    }

    public static int[][][] dp;
    public static int solve(int mask, int redempty, int other) {
        other = Math.min(other, n*n);
        if (mask == (1<<n)-1) return 0;
        if (dp[redempty][other][mask] != -1) return dp[redempty][other][mask];
        int ret = 1 << 29;
        for (int i = 0; i < n; i++) {
            if (((mask>>i)&1) == 1) continue;
            int pmask = mask | (1 << i);
            int havered = redempty == 1 ? 0 : other;
            int haveblue = redempty == 0 ? 0 : other;
            int cardred = countred[mask], cardblue = countblue[mask];

            int nred = Math.max(0, r[i]-(cardred+havered));
            int nblue = Math.max(0, b[i]-(cardblue+haveblue));
            int needmoves = Math.max(nred, nblue);
            int nextred = havered + needmoves - Math.max(0, r[i] - cardred);
            int nextblue = haveblue + needmoves - Math.max(0, b[i] - cardblue);

            if (nextred == 0) {
                ret = Math.min(ret, needmoves + solve(pmask, 1, nextblue));
            }
            if (nextblue == 0) {
                ret = Math.min(ret, needmoves + solve(pmask, 0, nextred));
            }
        }
        return dp[redempty][other][mask] = ret;
    }
}

Hongcow Draws a Circle

First to check if an answer can be arbitrarily large, we can see if there is any red point that is on the convex hull of all our points. So from now on, we can assume the answer is finite.

We can show that the optimal circle must touch a blue point. To see this, consider any optimal circle that doesn't touch a blue point. We can make it slightly bigger so that it does touch one.

So, let's binary search for the answer. However, you have to very careful and notice that the binary search isn't monotonic if we only consider circles touching blue points. However, if we consider circles that touch either a red or blue point, then the binary search is monontonic, so everything works out.

To check if a radius works, we can do a angle sweep around our center point. We have a fixed radius and fixed center, so each other point has at most two angles where it enters and exits the circle as we rotate it about the center point. We can keep track of these events and find an interval where the circle only contains red points.

import java.io.*;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.StringTokenizer;

public class RedAndBluePoints {
    public static double EPS = 1e-9;
    public static int PENALTY = 1000000;
    public static int n,m;
    public static long[] x, y;
    public static double[][] d;
    public static void main (String[] args) {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out, true);

        n = in.nextInt();
        m = in.nextInt();
        x = new long[n+m];
        y = new long[n+m];
        d = new double[n+m][n+m];
        Point[] ps = new Point[n+m];
        for (int i = 0; i < n+m; i++) {
            x[i] = in.nextInt();
            y[i] = in.nextInt();
            ps[i] = new Point(x[i], y[i]);
        }
        ps = convexHull(ps);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < ps.length; j++) {
                if (onSegment(ps[j], ps[(j+1)%ps.length], new Point(x[i],y[i]))) {
                    out.println(-1);
                    out.close();
                    System.exit(0);
                }
            }
        }


        for (int i = 0; i < n+m; i++) {
            for (int j = 0; j < n+m; j++) {
                d[i][j] = (x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]);
            }
        }

        double lower = 0;
        for (int startpoint = 0; startpoint < n+m; startpoint++) {
            if (!ok(startpoint, lower)) continue;
            double add = 20;
            int iter = 30;
            while (ok(startpoint, lower+2*add)) {
                add *= 2;
                iter++;
            }
            double lo = lower;
            double hi = lower+2*add;
            while (hi - lo > 1e-8 && iter-->0) {
                double mid = (lo + hi) / 2.0;
                if (ok(startpoint, mid)) lo = mid;
                else hi = mid;
            }
            lower = lo;
        }
        out.printf("%.10f\n", lower);
    }

    public static boolean ok(int center, double rad) {
        ArrayList<State> w = new ArrayList<>();
        int cur = center < n ? 1 : 0;
        for (int j = 0; j < n+m; j++) {
            if (j == center) continue;
            double reach = 2 * rad;
            if (reach * reach < d[center][j] + EPS) continue;

            double[] q = getAngles(center, j, rad);
            int add = j < n ? 1 : -PENALTY;
            if (q[1] < q[0]) cur += add;
            w.add(new State(q[0] - EPS, add));
            w.add(new State(q[1] + EPS, -add));
        }
        Collections.sort(w);
        int res = cur;
        for (State s : w) {
            cur += s.inc;
            res = Math.max(res, cur);
        }
        return res >= 1;
    }

    // returns two angles tangent to point i1 and point i2 with radius.
    public static double[] getAngles(int i1, int i2, double rad) {
        double D = d[i1][i2];
        double c = D/2.0;
        double b = Math.sqrt(D*rad*rad-c*c);
        double nx = (x[i2] - x[i1]) / D, ny = (y[i2] - y[i1]) / D;
        double bx = -ny * b, by = nx * b;
        double ax = nx * c, ay = ny * c;

        return new double[] {
                Math.atan2(ay - by, ax - bx),
                Math.atan2(ay + by, ax + bx),
        };
    }

    public static class Point {
        public final long x, y;

        public Point(long x, long y) {
            this.x = x;
            this.y = y;
        }
    }
    public static Point[] convexHull(Point[] p) {
        int n = p.length;
        if (n <= 1)
            return p;
        Arrays.sort(p, (a, b) -> Long.compare(a.x, b.x) != 0 ? Long.compare(a.x, b.x) : Long.compare(a.y, b.y));
        Point[] h = new Point[n * 2];
        int cnt = 0;
        for (int i = 0; i < n; h[cnt++] = p[i++])
            while (cnt > 1 && cross(h[cnt - 2], h[cnt - 1], p[i]) >= 0)
                --cnt;
        for (int i = n - 2, t = cnt; i >= 0; h[cnt++] = p[i--])
            while (cnt > t && cross(h[cnt - 2], h[cnt - 1], p[i]) >= 0)
                --cnt;
        return Arrays.copyOf(h, cnt - 1 - (h[0].x == h[1].x && h[0].y == h[1].y ? 1 : 0));
    }

    static long cross(Point a, Point b, Point c) {
        return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
    }

    public static boolean onSegment(Point a, Point b, Point c) {
        // does c lie on segment ab
        return c.x >= Math.min(a.x, b.x) && c.x <= Math.max(a.x, b.x) &&
                c.y >= Math.min(a.y, b.y) && c.y <= Math.max(a.y, b.y) &&
                (c.x - a.x) * (c.y - b.y) == (c.x - b.x) * (c.x - a.y);
    }


    static class State implements Comparable<State> {
        public double angle;
        public int inc;
        public State (double angle, int inc) {
            this.angle = angle;
            this.inc = inc;
        }

        public int compareTo(State other) {
            if (angle < other.angle) return -1;
            if (angle > other.angle) return 1;
            return 0;
        }
    }

    static class InputReader {
        public BufferedReader reader;
        public StringTokenizer tokenizer;

        public InputReader(InputStream stream) {
            reader = new BufferedReader(new InputStreamReader(stream), 32768);
            tokenizer = null;
        }

        public String next() {
            while (tokenizer == null || !tokenizer.hasMoreTokens()) {
                try {
                    tokenizer = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    throw new RuntimeException(e);
                }
            }
            return tokenizer.nextToken();
        }

        public int nextInt() {
            return Integer.parseInt(next());
        }
    }
}

For the inversion solution, let's fix the blue point that our circle touches. Then, let's take the inversion around this point (i.e. https://en.wikipedia.org/wiki/Inversive_geometry). Now, circles that pass through our center points become lines, and the interior of those circles are in the halfplane not containing the center point. The radius of the circle is inversely proportional to the distance between our center point to the line after inversion.

So, we can say we want to solve the following problem after inversion. Find the closest line that contains no blue points in the halfplane facing away from our center point and at least one red point. We can notice that we only need to check lines that contain a blue point on the convex hull after inversion.

To make implementation easier, you can make the additional observation that the sum of all convex hull sizes will be linear through the process of the algorithm. Some intuition behind this observation is that only adjacent nodes in a delaunay triangluation can appear on the convex hull after inversion, so the sum is bounded by the number of edges in such a triangulation (of course, we do not need to explicitly find the triangulation).

#pragma comment(linker, "/STACK:1000000000")
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cassert>
#include <ctime>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <vector>
#include <list>
#include <deque>
#include <queue>
#include <sstream>
#include <iostream>
#include <algorithm>

using namespace std;

#define pb push_back
#define mp make_pair
#define fs first
#define sc second
#define double long double

const double pi = acos(-1.0);
const double eps1 = 1e-7;
const double eps2 = 1e-14;

double sqr(double x) {
    return x * x; 
}

struct pt {
	double x, y;

    pt(double x_ = 0.0, double y_ = 0.0) : x(x_), y(y_) {}
};

pt operator + (const pt& a, const pt& b) {
	return pt(a.x + b.x, a.y + b.y);
}

pt operator - (const pt& a, const pt& b) {
	return pt(a.x - b.x, a.y - b.y);
}

pt operator * (const pt& a, double k) {
	return pt(a.x * k, a.y * k);
}

struct line {
	double a, b, c;
	line(double a_ = 1.0, double b_ = 0.0, double c_ = 0.0): a(a_), b(b_), c(c_) {
		norm();
    }

	line(const pt& p1, const pt& p2) {
		a = p2.y - p1.y;
		b = p1.x - p2.x;
		c = -a * p1.x - b * p1.y;

		norm();
	}

	void norm() {
		double k = sqrt(sqr(a) + sqr(b));
		a /= k;
		b /= k;
		c /= k;
	}

	double dist(const pt& p) const {
		return a * p.x + b * p.y + c;
	}
};
bool cmp (pt a, pt b) {
	return (a.x < b.x) || (a.x == b.x && a.y < b.y);
}

bool cw (pt a, pt b, pt c) {
	return a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y) < -eps2;
}

bool ccw (pt a, pt b, pt c) {
	return a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y) > eps2;
}

void convex_hull (vector<pt> & a) {
	if (a.size() == 1)  return;
    if (a.size() == 2) return;
	sort (a.begin(), a.end(), &cmp);
	pt p1 = a[0],  p2 = a.back();
	vector<pt> up, down;
	up.push_back (p1);
	down.push_back (p1);
	for (size_t i=1; i<a.size(); ++i) {
		if (i==a.size()-1 || cw (p1, a[i], p2)) {
			while (up.size()>=2 && !cw (up[up.size()-2], up[up.size()-1], a[i]))
				up.pop_back();
			up.push_back (a[i]);
		}
		if (i==a.size()-1 || ccw (p1, a[i], p2)) {
			while (down.size()>=2 && !ccw (down[down.size()-2], down[down.size()-1], a[i]))
				down.pop_back();
			down.push_back (a[i]);
		}
	}
	a.clear();
	for (size_t i=0; i<up.size(); ++i)
		a.push_back (up[i]);
	for (size_t i=down.size()-2; i>0; --i)
		a.push_back (down[i]);
}

int sign(double x) {
    if (fabs(x) < eps2)
        return 0;
    if (x > 0)
        return 1;
    return -1;
}

int main() {
    //freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);

    int n, m;

    cin >> n >> m;

    vector <pt> red(n), blue(m);
    for (int i = 0; i < n; i++) {
        cin >> red[i].x >> red[i].y;
    }

    for (int i = 0; i < m; i++) {
        cin >> blue[i].x >> blue[i].y;
    }

    if (m == 1) {
        cout << -1 << endl;
        return 0;
    }
    vector <pt> cvx_blue = blue;
    convex_hull(cvx_blue);
    int k = cvx_blue.size();
        
    for (int i = 0; i < n; i++) {
        bool flag = true;
        for (int j = 0; j < k; j++) {
            line hl(cvx_blue[j % k], cvx_blue[(j + 1) % k]);
            if (hl.dist(red[i]) > eps1) {
               flag = false;    
            }
        }

        if (flag) { 
            cout << -1 << endl;
    
            return 0;
        }

    }


    double ans = 0.0;

    for (int i = 0; i < m; i++) {
        vector <pt> new_blue;
        for (int j = 0; j < i; j++) {
            new_blue.pb(blue[j] - blue[i]);
            double d = sqr(new_blue.back().x) + sqr(new_blue.back().y);
            new_blue.back().x /= d;
            new_blue.back().y /= d;
        }

        new_blue.pb(pt(0.0, 0.0));

        for (int j = i + 1; j < m; j++) {
            new_blue.pb(blue[j] - blue[i]);
            double d = sqr(new_blue.back().x) + sqr(new_blue.back().y);
            new_blue.back().x /= d;
            new_blue.back().y /= d;
        }

        vector <pt> new_red;
        for (int j = 0; j < n; j++) {
            new_red.pb(red[j] - blue[i]);
            double d = sqr(new_red.back().x) + sqr(new_red.back().y);
            new_red.back().x /= d;
            new_red.back().y /= d;        
        }

        convex_hull(new_blue);

        int k = new_blue.size();
        int p = new_red.size();

        for (int j = 0; j < k; j++) {
            bool flag = false;
            line hl(new_blue[j], new_blue[(j + 1) % k]);
           
            for (int q = 0; q < p; q++) {
                if (hl.dist(new_red[q]) < eps2)
                    flag = true;            
            }            

            if (flag) {
                if (abs(hl.dist(pt(0.0, 0.0))) < eps2) {
                    cout << -1 << endl;
                    
                    return 0;
                }
    //            cerr << hl.dist(pt(0.0, 0.0)) << endl;
                /*
                if (fabs(hl.dist(pt(0.0, 0.0))) < eps) {
                    cout << -1 << endl;
                    return 0;
                }
                */
                ans = max(ans, 1.0 / abs(hl.dist(pt(0.0, 0.0))));
            }
        }

        for (int q = 0; q < p; q++) {
            for (int j = 0; j < k; j++) {
                line hl(new_red[q], new_blue[j]);
                if (sign(hl.dist(new_blue[(j + 1) % k])) * sign(hl.dist(new_blue[(j + k - 1) % k])) >= 0) {
                    if (abs(hl.dist(pt(0.0, 0.0))) < eps2) {
                        cout << -1 << endl;
                
                        return 0;
                    }

  //                  cerr << hl.dist(pt(0.0, 0.0)) << endl;
                    ans = max(ans, 1.0 / abs(hl.dist(pt(0.0, 0.0))));
                }
            }
        }
    }

    cout.precision(20);
    cout << ans / 2.0 << endl; 

    return 0;
}

Hongcow Masters the Cyclic Shift

Let M denote the total number of characters across all strings.

Consider how long it takes to compute f(L) for a single list.

Consider a graph where nodes are suffixes of strings. This means we already spelled out the prefix, and still need to spell out the suffix.

There are at most M nodes in this graph. Now, draw at most N edges connecting suffixes to each other. We can find the edges efficiently by doing suffix arrays or z algorithm or hashes.

Now, we claim is the list is good if and only if there is no cycle in this graph. You can notice that a cycle exists => we can construct a bad word. Also, if a bad word exists => we can form a cycle. So, we can check if there is a cycle, which takes O(N*M) time.

Next step is to notice that extending a bad list will never make it good. So we can do two pointers to find all good intervals, which requires O(n) calls to the check function. So, overall this runs in O(N^2*M) time.

You might be wondering why this problem asks for sublists rather than the entire list. To be honest, it's just to make tests slightly stronger (i.e. I get ~30^2x the number of tests in the same amount of space).

import java.io.*;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;

public class CyclicShiftsAgainAgain {
    public static int n;
    public static String[] s;
    public static int[] len;
    public static void main (String[] args) {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out, true);
        n = in.nextInt();
        s = new String[n+1];
        len = new int[n+1];
        s[0] = "";
        len[0] = 0;
        for (int i = 1; i <= n; i++) {
            s[i] = in.next();
            len[i] = len[i-1] + s[i].length();
        }

        int ans = 0;
        int front = 0;
        for (int i = 1; i <= n; i++) {
            while (!isGood(front+1, i)) front++;
            ans += i - front;
        }

        out.println(ans);
        out.close();
        System.exit(0);
    }

    public static boolean isGood(int from, int to) {
        if (from > to) return true;
        int numnodes = len[to] - len[from - 1];
        ArrayList<Integer>[] graph = new ArrayList[numnodes+1];
        for (int i = 0; i <= numnodes; i++) graph[i] = new ArrayList<>();
        for (int startword = from; startword <= to; startword++) {
            graph[numnodes].add(len[startword-1] - len[from-1]);
            StringBuilder sb = new StringBuilder();
            sb.append(s[startword]);
            sb.append("$");
            for (int k = from; k <= to; k++) {
                if (k == startword) continue;
                sb.append(s[k]);
                sb.append("#");
            }
            int[] z = zz(sb.toString().toCharArray());

            int curchar = 0;
            for (int i = 1; i < s[startword].length(); i++) {
                if (z[i] + i >= s[startword].length()) {
                    graph[i + len[startword-1] - len[from -1]].add(z[i] + len[startword-1] - len[from-1]);
                }
            }
            int curword = startword == from ? (from+1) : from;
            for (int i = s[startword].length()+1; i+1 < z.length; i++) {
                if (sb.charAt(i) == '#') {
                    i++;
                    curword++;
                    if (curword == startword) curword++;
                    curchar = 0;
                }

                int curnode = curchar + len[curword-1] - len[from-1];
                if (z[i] + curchar >= s[curword].length()) {
                    if (z[i] == s[startword].length()) {
                        if (curchar != 0) graph[curnode].add(numnodes);
                    } else {
                        graph[curnode].add(z[i] + len[startword-1] - len[from-1]);
                    }
                } else if (z[i] == s[startword].length()) {
                    graph[curnode].add(curnode + z[i]);
                }
                curchar++;
            }

        }
        return isDAG(graph);
    }

    public static int[] zz(char[] let) {
        int N = let.length;
        int[] z = new int[N];
        int L = 0, R = 0;
        for (int i = 1; i < N; i++) {
            if (i > R) {
                L = R = i;
                while (R < N && let[R - L] == let[R])
                    R++;
                z[i] = R - L;
                R--;
            } else {
                int k = i - L;
                if (z[k] < R - i + 1)
                    z[i] = z[k];
                else {
                    L = i;
                    while (R < N && let[R - L] == let[R])
                        R++;
                    z[i] = R - L;
                    R--;
                }
            }
        }
        z[0] = N;
        return z;
    }

    private static boolean isDAG(ArrayList<Integer>[] graph) {
        int n = graph.length;
        int[] indeg = new int[n];
        for (int i = 0; i < n; i++) for (int x : graph[i]) indeg[x]++;
        int[] queue = new int[n];
        int front = 0, back = 0, idx = 0;

        for (int i = 0; i < indeg.length; i++)
            if (indeg[i] == 0)
                queue[back++] = i;

        while (front != back) {
            int node = queue[front++];
            for (int next : graph[node]) {
                if (--indeg[next] == 0) {
                    queue[back++] = next;
                }
            }
        }

        return front == n;
    }

    static class InputReader {
        public BufferedReader reader;
        public StringTokenizer tokenizer;

        public InputReader(InputStream stream) {
            reader = new BufferedReader(new InputStreamReader(stream), 32768);
            tokenizer = null;
        }

        public String next() {
            while (tokenizer == null || !tokenizer.hasMoreTokens()) {
                try {
                    tokenizer = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    throw new RuntimeException(e);
                }
            }
            return tokenizer.nextToken();
        }

        public int nextInt() {
            return Integer.parseInt(next());
        }
    }
}

Hello everyone!

Codeforces round #385 will take place at the unusual usual time of Saturday, 17 December 19:35 MSK.

Thanks to the following people for making this round possible.

• LiChenKoh, xiaowuc1 for helping develop problems and discussing ideas with me.
• winger, AlexFetisov for testing the problems
• GlebsHP for all his valuable help with the round.
• MikeMirzayanov for the great Codeforces and Polygon platforms.

As usual, contestants will have 2 hours to solve 5 problems. Hope you will enjoy the problems!

Scoring will be announced closer before the round.

EDIT: It may be helpful to read the Interactive Problem Guide before the round for both divisions.

EDIT 2: The scoring distribution will be unusual:

Div2: 500-1000-1500-2250-2750

Div1: 500-1250-1750-2250-2500

EDIT 3: While you wait for system testing, here is a quick editorial: http://codeforces.net/blog/entry/49126

EDIT 4: Congratulations to the winners!

Div1:

1. tourist
2. Petr
3. PavelKunyavskiy
4. YuukaKazami
5. W4yneb0t

Div2:

1. Akulen
2. RVS
3. tpablo
4. theodor.moroianu
5. YouAndI

Hello everyone

I would like to invite you all to the last HackerEarth Clash of the year starting in around 28 hours (link to register here, check your time zone here). The contest will last 24 hours.

There will be five algorithmic problems and one approximation (optimization) problem. Read the problems for details on partial scoring for easier subtasks. I tried to make this clash slightly easier than my previous clashes, so hopefully there will be more than 1 perfect score on the algorithm problems. I hope you find the problems interesting nonetheless.

I would like to thank usaxena95 for all his help in testing, editing statements, and writing editorials, and belowthebelt for all his help with the round.

There will be prizes — t-shirts and Amazon gift cards.

Hope to see you all at the contest!

Hello everyone!

I would like to invite you to participate in HackerEarth August Circuits. It's a long contest that will start on August 20, 21:00 IST (check your timezone). Contest will run for 8 days.

The problemset consists of 7 traditional algorithmic tasks and 1 approximate problem. For traditional algorithmic tasks, you will receive points for every test case your solution passes — so you can get some points with partial solutions as well. For the approximation task, your score depends on the best solution in the contest so far. Check contest page for more details about in-contest schedule and rules.

I'm the tester of a problemset you'll have to work on — thanks to belowthebelt, jtnydv25, mgch, RomaWhite for preparing these tasks.

As usual, there will be some nice prizes for the top five competitors:

1. $100 Amazon gift card + HE t-shirt.
2. $75 Amazon gift card + HE t-shirt.
3. $50 Amazon gift card + HE t-shirt.
4. HE t-shirt.
5. HE t-shirt.

Good luck to everyone, and I hope to see you at the contest :)

Congratulations to the winners: 6 way tie for first place: mugurelionut, uwi, ceilks, Catalin Stefan Tiseanu, anta, Rafaël Bocquet

Unfortunately, the approximate problem was not very good at distinguishing top contestants (this was my fault with coming up with a weak generator). For prizes, we will evenly distribute prizes of the among the top 6. More specifically, the top 6 will each receive a $35 amazon gift card and a t-shirt.

I hope you enjoyed the contest! Let me know if you find any errors below. Thanks for participating.

Short solutions:

• Slime Combining: You can just do what's described in the statement. Or, maybe you can do something with the binary representation of the number.
• Guess the permutation: Find out where 1 should go. Then, find out where 2 should go, and so on.
• Constellation: Start with a triangle and break it up. Or, choose a point and look at angles. Or, sort by x coordinate.
• Hamiltonian Spanning Tree: Two cases: X > Y and X <= Y. For X > Y we can almost always avoid the spanning tree edges. For X <= Y we can do something greedy.
• Robot Arm: Make a segment tree on segments. A segment is basically just a linear transformation, which can be described with three numbers.
• Double Knapsack: Make the problem harder. Let's say I want a consecutive sublist of both lists that have equal sums. Then use pigeonhole principle to get an answer.
• Combining Slimes: Use conditional expectations. Define E[value of squares i .. n | i-th square has value j, and will not be merged with anything]. Notice that it's almost impossible for us to get a slime with value >= 50. Then, somehow generalize to large values of n (either by linear interpoloation or matrix exponentiation).

Long solutions:

Slime Combining

We can simulate the process described in the problem statement. There are many possible implementations of this, so see the example code for one possible implementation. This method can take O(n) time.

However, there is a faster method. It can be shown that the answer is simply the 1-based indices of the one bits in the binary representation of n. So, we can just do this in O(log n) time.

Example code (for simulation): http://codeforces.net/contest/618/submission/15669470

Example code (for faster method): http://codeforces.net/contest/618/submission/15669458

Guess the Permutation

One solution is to look for the column/row that contains only 1s and 0s. We know that this index must be the index for the element 1. Then, we can repeat this for 2 through n. See the example code for more details. The runtime of this solution is O(n^3).

However, there is an easier solution. One answer is to just take the max of each row, which gives us a permutation. Of course, the element n-1 will appear twice, but we can replace either occurrence with n and be done. See the other code for details

Example code (for first): http://codeforces.net/contest/618/submission/15669492

Example code (for second): http://codeforces.net/contest/618/submission/15669483

Comment: Originally, I wanted to set it so it wasn't guaranteed that there was a solution. But this seemed a bit tedious to me, so I didn't include this case.

Constellation

There are many possible solutions to this problem.

The first solution is to choose any nondegenerate triangle. Then, for each other point, if it is inside the triangle, we can replace one of our three triangle points and continue. We only need to make a single pass through the points. We need to be a bit careful about collinear points in this case.

Another solution is as follows. Let's choose an arbitrary point. Then, sort all other points by angle about this point. Then, we can just choose any two other points that have different angles, breaking ties by distance to the chosen point. (or breaking ties by two adjacent angles).

Example code (by breaking up triangles): http://codeforces.net/contest/618/submission/15669502

Example code (by angles): http://codeforces.net/contest/618/submission/15669511

Comment: Except for the second sample, all pretests didn't have collinear points. So many hacking cases are cases with collinear points.

Hamiltonian Spanning Tree

This is two separate problems: One where X > Y and when X <= Y.

Suppose X > Y. Then, we can almost always choose a path that avoides any spanning tree edges. There is one tricky case, which is the case of a star graph.

To prove the above statement, we know a tree is bipartite, so let's choose a bipartition X,Y. As long as there is exists a pair x in X and y in Y such that there isn't an edge between x and y, we can form a hamiltonian path without visiting any spanning tree edges (i.e. travel through all vertices in X and end at x, then go to y, then travel through all vertices in Y). We can see that this happens as long as it is not a complete bipartite graph, which can only happen when |X| = 1 or |Y| = 1 (which is the case of a star graph).

For the other case, X <= Y. Some intuition is that you want to maximize the number of edges that you use within the spanning tree. So, you might think along the lines of a "maximum path cover". Restating the problem is a good idea at this point.

Here's a restated version of the problem. You're given a tree. Choose the maximum number of edges such that all nodes are incident to at most 2 edges. (or equivalent a "2-matching" in this tree). Roughly, the intuition is that a 2-matching is a path cover, and vice versa.

This can be done with a tree dp, but here is a greedy solution for this problem. Root the tree arbitrarily. Then, let's perform a dfs so we process all of a node's children before processing a node. To process a node, let's count the number of "available" children. If this number is 0, then mark the node as available. If this number is 1, draw an edge from the node to its only available child and mark the node as available. Otherwise, if this number is 2 or greater, choose two arbitrary children and use those edges. Do not mark the node as available in this case.

Now, let U be the number of edges that we used from the above greedy algorithm. Then, the final answer is (n-1-U)*y + U*x).

(Proof may be added later, as mine is a bit long, unless someone has an easier proof they want to post).

Example code: http://codeforces.net/contest/618/submission/15669516

Comment: The case where X > Y and the tree is a star was not included in pretests. Thus, this could have been used to hack.

Robot Arm

We can view a segment as a linear transformation in two stages, first a rotation, then a translation.

We can describe a linear transformation with a 3x3 matrix, so for example, a rotation by theta is given by the matrix {{cos(theta), sin(theta), 0}, {-sin(theta), cos(theta), 0}, {0, 0, 1}} and a translation by L units is, {{1, 0, L}, {0, 1, 0}, {0, 0, 1}} (these can also be found by searching on google). So, we can create a segment tree on the segments, where a node in the segment tree describes the 3x3 matrix of a range of nodes. Thus updating takes O(log n) time, and getting the coordinates of the last blue point can be taken.

Some speedups. There is no need to store a 3x3 matrix. You can instead store the x,y, and angle at each node, and combine them appropriately (see code for details). Also, another simple speedup is to precompute cos/sin for all 360 degrees so we don't repeatedly call these functions.

Example code (Java): http://codeforces.net/contest/618/submission/15669521

Example code (C++): http://codeforces.net/contest/618/submission/15669530

Comment: I'm very sorry about precision issues. We realized this at the last minute, and I didn't expect so many solutions to fail because of this. I have checked my own answers against a BigDecimal implementation in Java, so try to use long doubles. Also, as a side note, this is the first ever data structure question that I've written.

Double Knapsack

Let's replace "set" with "array", and "subset" with "consecutive subarray".

Let a_i denote the sum of the first i elements of A and b_j be the sum of the first j elements of B. WLOG, let's assume a_n ≤ b_n. For each a_i, we can find the largest j such that b_j ≤ a_i. Then, the difference a_i - b_j will be between 0 and n - 1 inclusive. There are (n + 1) such differences (including a₀ - b₀), but only n integers it can take on, so by pigeon hole principle, at least two of them are the same.

So, we have a_i - b_j = a_i' - b_j'. Suppose that i' < i. It can be shown that j' < j. So, we rearranging our equation, we have a_i - a_i' = b_j - b_j', which allows us to extract the indices.

Example code: http://codeforces.net/contest/618/submission/15669546

Comment: It seemed difficult for me to generate strong cases. Is there an easy way to do it? I tried my best, but there may be some weird solutions that can pass that I just overloooked.

Combining Slimes

The probability that we form a slime with value i roughly satisfies the recurrence p(i) = p(i-1)^2, where p(1) and p(2) are given as base cases, where they are at most 999999999/1000000000. Thus, for i bigger than 50, p(i) will be extremely small (about 1e-300), so we can ignore values bigger than 50.

Let a[k][i] be the probability that a sequence of 1s and 2s can create i given that we have k squares to work with, and b[k][i] be the same thing, except we also add the constraint that the first element is a 2.

Then, we have the recurrence a[k][i] = a[k][i-1] * a[k-1][i-1], b[i][k] = b[k][i-1] * b[k-1][i-1] Note that as k gets to 50 or bigger a[k] will be approximately a[k-1] and b[k] will be approximately b[k-1] so we only need to compute this for the first 50 rows.

We can compute the probability that the square at i will have value exactly k as a[n-i][k] * (1 — a[n-i-1][k]).

Let dp[i][j] denote the expected value of the board from square i to n given that there is currently a slime with value j at index i and this slime is not going to be combined with anything else.

The final answer is just

We can compute dp[i][j] using 2 cases:

First, we compute this dp manually from n to n-50. After that, we can notice that since a[k] is equal to a[k-1] and b[k] is equal to b[k-1] for k large enough, this dp can be written as a matrix exponentiation with 50 states. Thus, this takes O(50^3 * log(n)).

Another approach that would also work is that after a large number of squares, the probabiltiy distribution of a particular square seems to converge (I'm not able to prove this though, though it seems to be true). So, by linearty of expectation, adding a square will add the same amount. So, you can do this dp up to maybe 500 or 1000, and then do linear interpolation from there.

Example code (with matrix exponentiation): http://codeforces.net/contest/618/submission/15669558

Example code (with linear interpolation): http://codeforces.net/contest/618/submission/15669560

Comments; This problem is inspired from the game 2048. The way I discovered these formulas was through some trial and error and comparing versus a bitmask dp. Try to come up with the bitmask dp solution first if you are having trouble with understanding the editorial.

Привет, Codeforces!

Приглашаю вас принять участие в особом раунде Codeforces, который начнется 29-го января в 20:05 (московское время). Спасибо, Wunder Fund — лучшие участники получат призы и сувениры! Вот несколько слов непосредственно от компании Wunder Fund:

Мы работаем в центре Москвы и занимаемся высокочастотным трейдингом — разрабатываем высокопроизводительные системы и алгоритмы автоматизированной торговли на финансовых рынках.

Именно здесь оказываются важны алгоритмы, которые вы так любите придумывать и реализовывать — нужно быть быстрее других, сделки совершаются за доли секунд! На Codeforces разделяют нашу любовь к высокой производительности, поэтому мы и решили провести раунд. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.

Мы предлагаем интересные и сложные задачи по low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь. У нас небольшая команда, поэтому вы сразу станете ее значительной частью. Разбираться в экономике и финансах не требуется, а вот алгоритмы и структуры данных это то, что нам нужно.

Заинтересовались? Присоединяйтесь к нам! Про вакансии можно почитать на нашем cайте.

Мы будем рады подарить участникам призы и подарки:

• 1 место — PlayStation 4
• 2 место — Xbox One
• 3-5 места — Sega MegaDrive 16bit c играми
• 1-50 места — сувенирные футболки Wunder Fund
• 51-500 места — 50 футболок будут распределены случайным образом!

А я хочу поблагодарить всех тех, кто помогал с подготовкой раунда:

• GlebsHP за ревью и помощь в подготовку задач,
• LiChenKoh и ??? за тестирование задач,
• Delinur за переводы,
• MikeMirzayanov за существование систем Codeforces и Polygon,
• и, конечно, Wunder Fund за инициативу выступить спонсором раунда!

Надеюсь всех вас увидеть на раунде. Желаю удачи и удовольствия от раунда!

Div2A: Kyoya and Photobooks

Solving this problem just requires us to simulate adding every character at every position at the string, and removing any duplicates. For instance, we can use a HashSet of Strings in Java to do this (a set in C++ or Python works as well).

Bonus: Prove that the number of ways is always (length of string + 1) * 25 + 1.

Example code: http://codeforces.net/contest/554/submission/11767578

Div2B: Ohana Cleans Up

For each row, there is only one set of columns we can sweep so it becomes completely clean. So, there are only n configurations of sweeping columns to look at. Checking a configuration takes O(n²) time to count the number of rows that are completely clean. There are n configurations in all, so this takes O(n³) time total.

Alternatively, another way of solving this problem is finding the maximum number of rows that are all the same.

Example code: http://codeforces.net/contest/554/submission/11767576

Div2C/Div1A: Kyoya and Colored Balls

Let f_i be the number of ways to solve the problem using only the first i colors. We want to compute f_n.

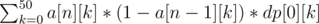
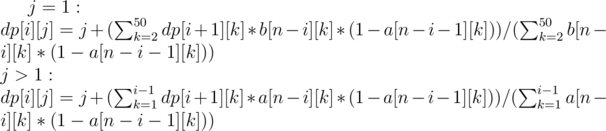
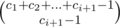Initially, we have f₁  =  1, since we only have a single color, and balls of the same color are indistinguishable. Now, to go from f_i to f_i + 1, we note that we need to put at a ball of color i + 1 at the very end, but the other balls of color i + 1 can go anywhere in the sequence. The number of ways to arrange the balls of color i + 1 is (minus one because we need to put one ball at the very end). 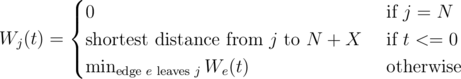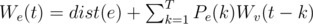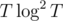Using this recurrence, we can solve for f_n.

Thus, we need to precompute binomial coefficients then evaluate the product.

Example code: http://codeforces.net/contest/553/submission/11767584

Div2D/Div1B: Kyoya and Permutation

Solving this requires making the observation that only swaps between adjacent elements are allowed, and all of these swaps must be disjoint. This can be discovered by writing a brute force program, or just noticing the pattern for small n.

Here's a proof for why this is. Consider the cycle that contains n. Since n is the largest number, it must be the last cycle in the sequence, and it's the first element of the sequence. If this cycle is length 1, then we're obviously ok (we can always append (n) to the end). If the cycle is of length 2, we need n to be involved in a cycle with n - 1. Lastly, if the cycle is of length 3 or more, we will see we run into a problem. We'll only show this for a cycle of length 3 (though this argument does generalize to cycles of larger length). Let (nxy) be the cycle. So that means, n is replaced by x, x is replaced by y and y is replaced by n. So, in other words, the original permutation involving this cycle must look like

position:   ... y x n
number  :   ... n y x

However, we need it to look like (nxy) so this case is impossible.

So, once we know that n is a in a cycle of length 1 or 2, we can ignore the last 1 or 2 elements of the permutation and repeat our reasoning. Thus, the only valid cases are when we swap adjacent elements, and all swaps are disjoint. After making this observation, we can see the number of valid permutations of length n is fib(n+1). (to see this, write try writing a recurrence).

To reconstruct the kth permutation in the list, we can do this recursively as follows: If k is less than fib(n), then 1 must be the very first element, and append the kth permutation on {1,...,n-1} with 1 added everywhere. Otherwise, add 2, 1 to the very front and append the k-fib(n)th permutation on {1,...,n-2} with 2 added everywhere.

Example code: http://codeforces.net/contest/553/submission/11767583

Div2E/Div1C: Love Triangles

Let's look at the graph of characters who love each other. Each love-connected component can be collapsed into a single node, since we know that all characters in the same connected component must love each other.

Now, we claim that the resulting collapsed graph with the hate edges has a solution if and only if the resulting graph is bipartite.

To show this, suppose the graph is not bipartite. Then, there is an odd cycle. If the cycle is of length 1, it is a self edge, which clearly isn't allowed (since a node must love itself). For any odd cycle of length more than 1, let's label the nodes in the cycle a₁, a₂, a₃, ..., a_k. Then, in general, we must have a_i loves a_(i + 2), since a_i, a_(i + 1) hate each other and a_(i + 1), a_(i + 2) hate each other (all indicies taken mod k). However, we can use the fact that the cycle is odd and eventually get that a_i and a_i + 1 love each other. However, this is a contradiction, since we said they must originally hate each other.

For the other direction, suppose the graph is bipartite. Let X, Y be an arbitrary bipartition of the graph. If we let all nodes in X love each other and all nodes in Y love each other, and every edge between X and Y hate each other, then we get a solution. (details are omitted, though I can elaborate if needed).

Thus, we can see that we have a solution if and only if the graph is bipartite. So, if the graph is not bipartite, the answer is zero. Otherwise, the second part of the proof gives us a way to count. We just need to count the number of different bipartitions of the graph. It's not too hard to see that this is just simply 2^(number of connected components — 1) (once you fix a node, you fix every node connected to it).

This entire algorithm takes O(N + M) time.

Example code: http://codeforces.net/contest/553/submission/11767582

Div1D: Nudist Beach

The algorithm idea works as follows:

Start with all allowed nodes. Remove the node with the smallest ratio. Repeat. Take the best ratio over all iterations. It's only necessary to consider these subsets. Proof for why.

We say this process finds a ratio of at least p if and only if there exists a subset with ratio at least p.

Exists a subset with ratio at least p => algorithm will find answer of at least p. First, observe that the ratio of any particular node only decreases throughout the algorithm. Thus, all nodes in this subset initally have ratio at least p. Then, the very first node that gets removed from this subset must not have ratio smaller than p, thus the above algorithm will record an answer of at least p.

Exists no subset with ratio at least p => algorithm finds answer at most p. No subset with ratio at least p implies every subset has ratio at most p. Thus, at every iteration of our algorithm, we'll get an answer of at most p, so we're done.

Thus, we can see these are necessary and sufficient conditions, so we're done.

Now for efficient implementation, we can use a variant of Dijkstra's. Recording the best subset must be done a bit more carefully as well.

Example code: http://codeforces.net/contest/553/submission/11767581

Div1E: Kyoya and Train

The Naive solution is O(MT²). Let W_j(t) be the optimal expected time given we are at node j, with t time units left. Also, let W_e(t) be the optimal expected time given we use edge e at time t.

Now, we have

And, if e = (u->v), we have

Doing all this naively takes O(MT²).

Now, we'll speed this up using FFT. We'll focus on only a single edge for now. The problem here, however, is that not all W_v values are given in advance. Namely, the W_v values require us to compute the W_e values for all edges at a particular time, and vice versa. So we need some sort of fast "online" version of FFT.

We do this as follows. Let's abstract away the original problem, and let's say we're given two arrays a,b, where a is only revealed one at a time to us, and b is given up front, and we need to compute c, their convolution (in the original problem b is P_e, and a is W_v, and c is W_e). Now, when we get the ith value of a, we need to return the ith value of the convolution of c. We can only get the ith value of a when we compute the i-1th values of c for all c.

Split up b into a block of size 1, a block of size 1, then a block of size 2, then a block of size 4, then 8, and so on.

Now, we get a₀, which will allow us to compute c₁, which lets us get a₁, which allows us to compute c₂, and so on.

So, now we have the following:

b_1 | b_2 | b_3 b_4 | b_5 b_6 b_7 b_8 | ...

We'll describe the processing of a single a_i

When we get a_i, we will first convolve it with the first two blocks, and add those to the appropriate entry. Now, suppose a_i is multiple of a 2^k for some k. Then, we will convolve a_i - 2^k .. a_i - 1 with the block in b with the same size.

As an example.

      b_1 | b_2 | b_3 b_4 | b_5 b_6 b_7 b_8 | ...
a_0   a0b1  
            a0b2

This gives us c₀, which then allows us to get a₁

      b_1 | b_2 | b_3 b_4 | b_5 b_6 b_7 b_8 | ...
a_0   a0b1  a1b1
a_1         a0b2 a1b2

This gives us c₁, which then allows us to get a₂

a₂ is now a power of 2, so this step will also additionally convolve a₀, a₁ with b₃, b₄

      b_1 | b_2 | b_3      b_4    | b_5 b_6 b_7 b_8 | ...
a_0   a0b1  a1b1  a2b1
a_1         a0b2  a1b2    a2b2
a_2               a0b3 (a1b3+a0b4)  a1b4

So, we can see this gives us c₂, which then allowus to get a₃, and so on and so forth.

Thus, this process of breaking into blocks works. As for runtime, we run FFT on a block size of B T/B times, so this term contributes (T/B) * B log B = T log B

So, we sum T log 2 + T log 4 + ... + T log 2\^(log T) <= T log\^2 T

Thus, the overall time per edge is , which gives us a total runtime of .

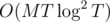Example code: http://codeforces.net/contest/553/submission/11767579

Hello Codeforces!

I invite all of you to participate in regular Codeforces round #309 that will take place on 24 June, 19:30 MSK.

Some of you may know me as lg5293 on Topcoder (you can see some of my past problems here), but this is my first time ever writing a Codeforces round. I've designed all the problems myself and I hope you enjoy them.

I want to thank ctunoku for helping me come up with stories for the problems, Zlobober for his immense help with preparation for this round, winger for testing the problems, Delinur for translating statements, and of course MikeMirzayanov for the superb Codeforces and Polygon systems.

I hope to see you all at the round. Good luck and have fun! :)

UPD: Scoring will be dynamic. Problems will be arranged by what I think is increasing difficulty.

UPD: Editorial is here. Congratulations to the top 5:

Div 1:

1. ecnerwala

2. scott_wu

3. enot110

4. KADR

5. yeputons

Div2:

1. Elsa_Elsa

2. Chenyao

3. cdkrot

4. Shayan

5. M_H_M