
Привет, Codeforces!
Очередной сезон соревнований по программированию стартовал, и самое время поднять мотивацию многим из вас.
От лица фонда Botan Investment и его президента Виктора Шабурова хочу анонсировать уникальную акцию. Цель акции — поддержать и развить интерес к спортивному программированию в регионах России. Пока Москва и СПб исключены из списка, а студенты и выпускники вузов других городов могут получить приз: 50000 рублей и поездку в Сочи для знакомства с командами стартапов Botan Investment.
Для того, чтобы получить приз, ты должен:
- стать красным (гроссмейстером) на Codeforces и быть им на протяжении трех раундов подряд;
- учиться на 4-м или более курсе университета или быть выпускником вуза РФ;
- быть не старше 30 лет;
- быть готовым приехать в Сочи (разумеется, за наш счет) и очно подтвердить свои навыки на очередном раунде.
Более подробно об акции — на сайте Botan Investment.
Виктор, я думаю, не нуждается в представлении на Codeforces, потому как еще свеж в памяти Looksery Cup 2015.
Если ты уже готов — смело пиши на [email protected] по вопросам организации поездки.









 .
.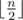 раз, то каждый ребенок может получить левую и правую варежки разного цвета. Для этого отсортируем все левые варежки в порядке убывания частоты их цвета: для входа 1 2 1 2 3 1 3 3 1 получилось бы 1 1 1 1 3 3 3 2 2. Чтобы получить последовательность цветов правых варежек, сдвинем последовательность цветов левых варежек влево на количество самого популярного цвета (в примере это 4, поэтому получим 3 3 3 2 2 1 1 1 1). И теперь объединим эти две последовательности в пары (1 — 3, 1 — 3, 1 — 3, 1 — 2, 3 — 2, 3 — 1, 3 — 1, 2 — 1, 2 — 1). Легко показать, что при этом все пары будут состоять из варежек различного цвета.
раз, то каждый ребенок может получить левую и правую варежки разного цвета. Для этого отсортируем все левые варежки в порядке убывания частоты их цвета: для входа 1 2 1 2 3 1 3 3 1 получилось бы 1 1 1 1 3 3 3 2 2. Чтобы получить последовательность цветов правых варежек, сдвинем последовательность цветов левых варежек влево на количество самого популярного цвета (в примере это 4, поэтому получим 3 3 3 2 2 1 1 1 1). И теперь объединим эти две последовательности в пары (1 — 3, 1 — 3, 1 — 3, 1 — 2, 3 — 2, 3 — 1, 3 — 1, 2 — 1, 2 — 1). Легко показать, что при этом все пары будут состоять из варежек различного цвета.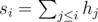 . Then the sum of heights of the planks
. Then the sum of heights of the planks 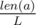 . Зафиксируем позицию
. Зафиксируем позицию 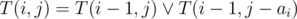 . Заметим, что
. Заметим, что 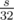 действий, поэтому выяснить, можно ли набрать сумму
действий, поэтому выяснить, можно ли набрать сумму 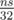 операций. Однако, тут нужно применить один трюк для того, чтобы восстановить, какие именно предметы нужно взять. Давайте для каждого значения суммы
операций. Однако, тут нужно применить один трюк для того, чтобы восстановить, какие именно предметы нужно взять. Давайте для каждого значения суммы 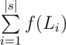 , где
, где 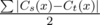 . Теперь жадно построим лексикографически наименьшее решение. Будет идти в порядке возрастания позиции подбирать, какой символ будет в этой позиции в ответе. Найдем первый в порядке возрастания символ, которые может стоять на этом месте в оптимальном ответе. Для того, чтобы быстро проверять, может ли символ стоять или нет, мы будем все время пересчитывать величины
. Теперь жадно построим лексикографически наименьшее решение. Будет идти в порядке возрастания позиции подбирать, какой символ будет в этой позиции в ответе. Найдем первый в порядке возрастания символ, которые может стоять на этом месте в оптимальном ответе. Для того, чтобы быстро проверять, может ли символ стоять или нет, мы будем все время пересчитывать величины 
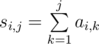 . Естественно, все частичные суммы надо посчитать за
. Естественно, все частичные суммы надо посчитать за 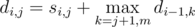 .
. 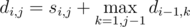 .
. 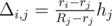 .
.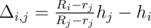 .
.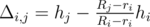 .
.
