Summary: This blog talks about solving two kinds of simple recursions: F(n + 1) = aF(n) + b and F(n + 1) = aF(n) + bF(n - 1)
1. Preliminary Knowledge
(1) The solution of recursion F(n + 1) = aF(n) is F(n) = an - 1F(1).
(2) The solution of recursion F(n + 1) = F(n) + a is F(n) = (n - 1)a + F(1).
(3) The recursion F(n + 1) = kF(n) is the same as F(n) = kF(n - 1), also F(n + 1) = aF(n) + bF(n - 1) is the same as F(n) = aF(n - 1) + bF(n - 2) in this blog.
2. Solving F(n + 1) = aF(n) + b, a, b are constants, a > 1
The main idea is to create another function G(n) that satisfy G(n) = kG(n - 1) with constant k, solve G(n), and then solve F(n).
F(n + 1) = aF(n) + b
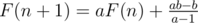
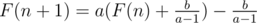
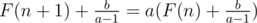
Let 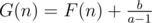 we have
we have
G(n) = aG(n - 1)
G(n) = an - 1G(1)
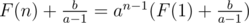
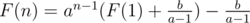
3. Solving F(n + 1) = aF(n) + bF(n - 1), a, b are constants
The main idea is also to create G(n), but the method is different, and the function G(n) is more complicated.
F(n + 1) = aF(n) + bF(n - 1)
Let α, β be two real numbers that satisfy α + β = a, αβ = - b, α ≤ β we have
F(n + 1) = (α + β)F(n) - αβF(n - 1)
F(n + 1) - αF(n) = βF(n) - αβF(n - 1)
F(n + 1) - αF(n) = β(F(n) - αF(n - 1))
Let G(n) = F(n + 1) - αF(n), also we have G(n - 1) = F(n) - αF(n - 1)
G(n) = βG(n - 1), therefore G(n + 1) = βG(n)
G(n) = βn - 1G(1)
F(n + 1) - αF(n) = βn - 1(F(2) - αF(1)) (1)
Similarly, because of F(n + 1) = (α + β)F(n) - αβF(n - 1) we have
F(n + 1) - βF(n) = αF(n) - αβF(n - 1)
F(n + 1) - βF(n) = α(F(n) - βF(n - 1))
Let H(n) = F(n + 1) - βF(n) we have H(n - 1) = F(n) - βF(n - 1)
H(n) = αH(n - 1), therefore H(n + 1) = αH(n)
H(n) = αn - 1H(1)
F(n + 1) - βF(n) = αn - 1(F(2) - βF(1)) (2)
Suppose that α ≠ β
(2) - (1) we have
(α - β)F(n) = αn - 1(F(2) - βF(1)) - βn - 1(F(2) - αF(1))
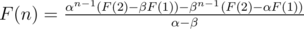
How to get the proper α, β?
According to the Vieta Theorem, α, β is the two solutions of quadratic equation x2 - ax - b = 0.
Of course, we only talk about α ≠ β, a2 ≠ - 4b.
Just solving the quadratic equation is OK. (You can get the formula for solving a quadratic equation from the problem 530A - Квадратное уравнение.)
This equation is called the characteristic equation.
Example: Solve the Fibonacci sequence F(1) = 1, F(2) = 1, F(n) = F(n - 1) + F(n - 2).
Solution: Here we have 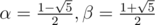
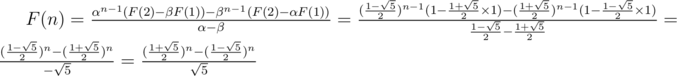
(because we have 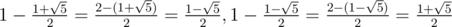 )
)
What will happen if α = β, a2 = 4b?
I am sorry that I cannot solve it yet.
I'll try to solve it later.
UPD: This method can be used to solve the recursions with lengths more than 2.
We replace the quadratic equation with an equation with higher degree, and do the same thing as quadratic.










Auto comment: topic has been updated by suncongbo (previous revision, new revision, compare).
This is simply math problem.
F(n + 1) - αF(n) = βn - 1(F(2) - αF(1))
This equation is as follows when α = β.
F(n + 1) - αF(n) = αn - 1(F(2) - αF(1))
If you divide both sides by αn + 1 and put G(n) = F(n) / αn, you can get the binomial recurrence formula like G(n + 1) = AG(n) + B.
F(n + 1) / αn + 1 - F(n) / αn = (F(2) - αF(1)) / α2
G(n + 1) - G(n) = (F(2) - αF(1)) / α2, G(1) = F(1) / α
G(n) = G(1) + (n - 1) × ((F(2) - vF(1)) / α2)
therefore,
F(n) = G(n) × αn = {(F(1) / α) + ((n - 1) × (F(2) - αF(1)) / α2)} × αn
Oh, I understand.
Thanks for your explaination.
Auto comment: topic has been updated by suncongbo (previous revision, new revision, compare).