632F - Magic Matrix

The problem was suggested by Lewin Gan Lewin. The solution and proof also belongs to him.

Consider the undirected complete graph with n nodes, with an edge between nodes i, j with cost a_ij. Let B_ij denote the minimum possible value of the max edge of a path from i to j. We know that a_ij ≥ B_ij by definition.

If the matrix is magic, we can choose arbitrary k₁, k₂, ..., k_m such that a_ij ≤ max(a_i, k1, a_k1, k2, ..., a_km, j) by repeating invocations of the inequality given. Also, you can show that if this inequality is satisfied, then the matrix is magic (by choosing an m = 1 and k₁ arbitrary).

So, this shows that the matrix is magic if and only if a_ij ≤ B_ij. Thus, combining with a_ij ≥ B_ij, we have a_ij = B_ij.

We need a fast way to compute B_ij for all pairs i, j. This can be computed as the MST, as the path in the MST minimizes the max edge between all pairs of nodes. So, the algorithm works as follows. First, find the MST on the complete graph. Then, the matrix is magic if and only if the max edge on the path between i, j in the MST is exactly equal to a_i, j. Also you shouldn't forget to check symmetry of the matrix and diagonal for zeros.

P.S.: Unfortunately we couldn't increase the value n in this problem: the tests already had the size about 67MB and they couldn't be given with generator. So most of the users who solved this problem uses bitset-s. The complexity of their solution is 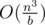, where b = 32 or b = 64.

C++ solution, binary lifts by me.

Java solution by Lewin.

Complexity: O(n²logn) or O(n²).