632A - Grandma Laura and Apples

Задача предложена пользователем unprost.

Рассмотрим на процесс с конца. Последний покупатель всегда покупает половину яблока и половину получает бесплатно (поэтому последняя строка на самом деле всегда равна halfplus). Далее каждый покупатель удваивает текущее количество яблок и возможно прибавляет к нему единицу. Таким образом, нам просто задано бинарное представление числа записанное с конца. Для подсчёта ответа нужно просто с конца восстанавливать количество яблок попутно, вычисляя сумму денег.

С++ solution by me.

С++ solution by unprost.

Сложность: O(p).

632B - Alice, Bob, Two Teams

Задача предложена пользователем Lewin Gan Lewin.

Посчитаем частичные суммы на префиксах отдельно для всех чисел (в массиве s1) и отдельно для чисел напротив, которых стоит буква B (в массиве s2). Теперь мы можем за O(1) вычислять сумму на любом подотрезке, а также сумму на любом отрезке по числам напротив буквы B.

Переберем теперь префикс или суффикс и посчитаем сумму в случае его изменения по формуле: sum(s1, 0, n - 1) + sum(s2, 0, i) - 2·sum(s1, 0, i) для префикса и sum(s1, 0, n - 1) + sum(s2, i, n - 1) - 2·sum(s1, i, n - 1) для суффикса.

C++ solution by me.

Python solution by Lewin.

Сложность: O(n).

632C - The Smallest String Concatenation

Задача предложена пользователем Lewin Gan Lewin. Доказательство транзитивности также принадлежит ему.

Отсортируем все строки по компаратору a + b < b + a и сконкатенируем их в получившемся порядке. Докажем, что ответ оптимальный. Пусть эта операция транзитивна (то есть из 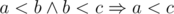). Рассмотрим оптимальный ответ в котором есть пара строк, находящихся по этому отношению в обратном порядке. Поскольку это отношение транзитивно, то без потери общности можно считать, что это пара соседних строк. Но тогда мы их можем просто поменять местами и улучшить ответ.

Докажем транзитивность отношения. Будем смотреть на эти строки как на числа в 26-ной системе счисления. Тогда отношения a + b < b + a эквивалентно 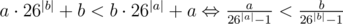. Последнее есть просто отношение для действительных чисел. Таким образом, мы доказали транзитивность отношения a + b < b + a.

C++ solution by me.

Python solution by Lewin.

P.S.: Удивительно но в этой задаче решение на Python работает более чем в 5 раз быстрее решения на С++. Если кто-нибудь понимает почему, пожалуйста поделитесь очень интересно.

Сложность: O(nLlogn), где L — наибольшая длина строки.

632D - Longest Subsequence

Задачу предложил Денис Безруков pitfall.

Пусть cnt_x количество повторений числа x в заданном массиве (понятно, что числа большие m можно не рассматривать). Переберём и 1 ≤ k, x·k ≤ m и увеличим значение в позиции k·x в некотором массиве z на величину cnt_x. Таким образом, значение z_l равно количеству чисел в исходном массиве делящих l. Найдём минимальное l с максимальным значением z_l (1 ≤ l ≤ m). Легко видеть, что ответом на задачу будут числа делящие l.

Оценим время работы решения. Количество пар (k, x) можно сверху оценить как .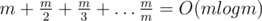

C++ solution by me.

Java solution by pitfall.

Сложность: O(n + mlogm).

632E - Thief in a Shop

Задачу предложил Алексей Чесноков CleRIC.

Пусть k = 2, тогда это стандартная задача которая может быть решена с помощью БПФ (быстрого преобразования Фурье). А решается она следующим образом: рассмотрим многочлен в которого коэффициент при i-й степени равен единице если и только если в заданном массиве есть число i. Возведём этот многочлен в квадрат, тогда те i коэффициент при которых в квадрате не равен 0 будут находиться в ответе. Легко обобщить это решение на случай произвольного k. Нужно просто исходный многочлен возвести в k-ю степень. Это, конечно, нужно сделать с помощью бинарного возведения в степень. Сложность получается O(WlogWlogk), где W — максимальная сумма.

Заметим, что это решение можно улучшить. Зачем возводить в степень многочлен, когда можно возводить в степень его образ (то есть его ДПФ)? Единственное, что нас может остановить это то, что в случае комплексного БПФ будут получаться очень большие числа (порядка 1000-х степеней) и соответственно никакие вещественные типа нас не спасут). Но это можно сделать в целых числах используя теоретикочисловое преобразование Фурье (ТПФ). У этого решения есть проблема, что при преобразовании (прямом или обратном) какие-то коэффициенты могут случайно обнулиться по модулю простого из ТПФ, но на самом деле коэффициент не ноль. Это можно обойти случайным выбором простого (а лучше двух или трёх), чтобы никто не мог взломать решение. Таким образом, получаем сложность O(W(logW + logk)).

Основное авторское решение было со сложностью O(WlogWlogk) с комплексным Фурье, второе с той же сложностью но по модулю, третье было с улучшенной асимптотикой (некоторые участники тоже это сдали можете попробовать взломать их, они вроде не выбирали модуль случайным образом).

С++ solution, complex FFT by me.

С++ solution, NTT by me.

С++ solution, improved NTT by me.

С++ solution by CleRIC.

P.S.: Чтобы решение было быстрым нужно каждый раз умножать многочлены нужной степени, а не степени 2²⁰.

Сложность: O(WlogWlogk) или O(W(logW + logk)), в зависимости от смелости кодера :-)

632F - Magic Matrix

Задача предложена пользователем Lewin Gan Lewin. Решение и доказательство также принадлежат ему.

Рассмотрим полный граф с весами рёбер a_ij. Обозначим B_ij — минимальное значение максимального ребра на пути из вершины i в вершину j. Очевидно a_ij ≥ B_ij по определение B_ij.

Если матрица волшебная мы можем выбрать произвольную последовательность k₁, k₂, ..., k_m и получить a_ij ≤ max{a_i, k1, a_k1, k2, ..., a_km, j} (для этого нужно последовательно применить третье неравенство для волшебной матрицы). Также легко показать, что если это условие выполнено, то матрицы волшебная (нужно просто взять m = 1 и выбрать произвольное k₁).

Таким образом, мы получили, что матрица волшебная тогда и только тогда, когда a_ij ≤ B_ij. Пользуясь неравенством a_ij ≥ B_ij окончательно получаем a_i, j = B_i, j.

Теперь нам нужно быстрый способ подсчёта значений B_ij для всех пар (i, j). Это можно сделать вычислым MST (минимальное покрывающее дерево графа), поскольку MST минимизирует максимальное ребро на путях между всеми парами вершин. Таким образом, решение выглядит следующим образом: сначала нужно найти MST (например, алгоритмом Прима за O(n²)), а затем нужно найти наибольшее ребро на пути из i в j и проверить, что оно равно a_ij (я это делал с помощью бинарного подъёма по дереву, но это можно делать во время построения MST). И, конечно, нужно не забыть предварительно проверить матрицу на симметричность и нули на диагонали.

P.S.: К сожалению в этой задаче мы не могли увеличить n, поскольку тесты здесь очень специфические (и уже имели размер порядка 67MB) и генератором их задавать было нельзя. Большинство решений, которые сдали участники на контесте использует bitset-ы и работает за 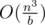, где b = 32 или b = 64.

C++ solution, binary lifts by me.

Java solution by Lewin.

Сложность: O(n²logn) или O(n²).