632A - Бабушка Лаура и яблоки
Задача предложена пользователем unprost.
Рассмотрим на процесс с конца. Последний покупатель всегда покупает половину яблока и половину получает бесплатно (поэтому последняя строка на самом деле всегда равна halfplus). Далее каждый покупатель удваивает текущее количество яблок и возможно прибавляет к нему единицу. Таким образом, нам просто задано бинарное представление числа записанное с конца. Для подсчёта ответа нужно просто с конца восстанавливать количество яблок попутно, вычисляя сумму денег.
С++ solution by me.
С++ solution by unprost.
Сложность: O(p).
632B - Алиса, Боб, две команды
Задача предложена пользователем Lewin Gan Lewin.
Посчитаем частичные суммы на префиксах отдельно для всех чисел (в массиве s1) и отдельно для чисел напротив, которых стоит буква B (в массиве s2). Теперь мы можем за O(1) вычислять сумму на любом подотрезке, а также сумму на любом отрезке по числам напротив буквы B.
Переберем теперь префикс или суффикс и посчитаем сумму в случае его изменения по формуле: sum(s1, 0, n - 1) + sum(s2, 0, i) - s·sum(s1, 0, i) для префикса и sum(s1, 0, n - 1) + sum(s2, i, n - 1) + 2·sum(s1, i, n - 1) для суффикса.
C++ solution by me.
Python solution by Lewin.
Сложность: O(n).
632C - Наименьшая конкатенация строк
Задача предложена пользователем Lewin Gan Lewin. Доказательство транзитивности также принадлежит ему.
Отсортируем все строки по компаратору a + b < b + a и сконкатенируем их в получившемся порядке. Докажем, что ответ оптимальный. Пусть эта операция транзитивна (то есть из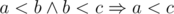 
). Рассмотрим оптимальный ответ в котором есть пара строк, находящихся по этому отношению в обратном порядке. Поскольку это отношение транзитивно, то без потери общности можно считать, что это пара соседних строк. Но тогда мы их можем просто поменять местами и улучшить ответ.
Докажем транзитивность отношения. Будем смотреть на эти строки как на числа в 26-ной системе счисления. Тогда отношения a + b < b + a эквивалентно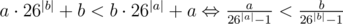 
. Последнее есть просто отношение для действительных чисел. Таким образом, мы доказали транзитивность отношения a + b < b + a.
C++ solution by me.
Python solution by Lewin.
P.S.: Удивительно но в этой задаче решение на Python работает более чем в 5 раз быстрее решения на С++. Если кто-нибудь понимает почему, пожалуйста поделитесь очень интересно.
Сложность: O(nLlogn), где L — наибольшая длина строки.
632D - Самая длинная подпоследовательность
Задачу предложил Денис Безруков pitfall.
Пусть cntx количество повторений числа x в заданном массиве (понятно, что числа большие m можно не рассматривать). Переберём 
и 1 ≤ k, x·k ≤ m и увеличим значение в позиции k·x в некотором массиве z на величину cntx. Таким образом, значение zl равно количеству чисел в исходном массиве делящих l. Найдём минимальное l с максимальным значением zl (1 ≤ l ≤ m). Легко видеть, что ответом на задачу будут числа делящие l.
Оценим время работы решения. Количество пар (k, x) можно сверху оценить как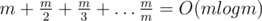 
.
C++ solution by me.
Java solution by pitfall.
Сложность: O(n + mlogm).
