Всем привет! Как вы уже, наверно, знаете (если не знаете — то советую узнать), в двумерной геометрии весьма удобно использовать комплексные числа для задания точек и вращений. Сейчас я хочу рассказать вам о похожей конструкции, которая позволяет эффективно работать с трёхмерным пространством. Базовые познания в аналитической геометрии желательны.
Итак, кватернион — это гиперкомплексное число, которое может быть представлено в виде 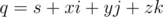 , где
, где 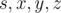 — действительные числа, а
— действительные числа, а 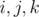 — мнимые единицы. На кватернионах может быть введена операция умножения, которая задана тождеством
— мнимые единицы. На кватернионах может быть введена операция умножения, которая задана тождеством  . Из этого тождества может быть выведена вся таблица умножения кватернионных единиц:
. Из этого тождества может быть выведена вся таблица умножения кватернионных единиц:
Отметим, что заданное таким образом кватернионное умножение обладает свойствами ассоциативности и дистрибутивности относительно сложения, в чём при желании можно убедиться, но не является коммутативным.
Четвёрку 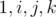 можно рассматривать как ортонормированный базис в четырёхмерном линейном пространстве, а кватернионы представлять в виде
можно рассматривать как ортонормированный базис в четырёхмерном линейном пространстве, а кватернионы представлять в виде 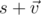 , где
, где 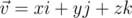 — вектор трёхмерного линейного пространства с базисом
— вектор трёхмерного линейного пространства с базисом 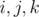 . Компоненты
. Компоненты  и
и 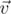 называются соответственно скалярной и векторной составляющими кватерниона. Пусть у нас есть кватернионы
называются соответственно скалярной и векторной составляющими кватерниона. Пусть у нас есть кватернионы 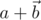 и
и 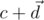 . Тогда их произведение можно посчитать как
. Тогда их произведение можно посчитать как 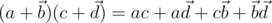 . Рассмотрим подробнее умножение двух чисто векторных кватернионов.
. Рассмотрим подробнее умножение двух чисто векторных кватернионов.
(x1i + y1j + z1k)(x2i + y2j + z2k) = - (x1x2 + y1y2 + z1z2) + i(y1z2 - z1y2) + j(z1x2 - x1z2) + k(x1y2 - y1x2).
Заметим, что это можно кратко переписать как 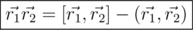 , где
, где 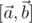 и
и  — соответственно векторное и скалярное произведения векторов
— соответственно векторное и скалярное произведения векторов 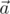 и
и 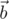 . Таким образом, окончательно получаем формулу для произведения кватернионов
. Таким образом, окончательно получаем формулу для произведения кватернионов  .
.
Наконец, обратим внимание, что кватернион 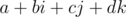 может также быть задан в виде
может также быть задан в виде 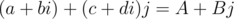 , где
, где 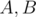 — комплексные числа. В таком случае произведение кватернионов
— комплексные числа. В таком случае произведение кватернионов 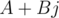 и
и 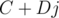 может быть записано как
может быть записано как 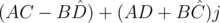 , где
, где  — сопряжённое к
— сопряжённое к  комплексное число.
комплексное число.
Покажем, что любой ненулевой кватернион обратим. Действительно, по аналогии с комплексными числами можно рассмотреть для кватерниона 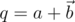 кватернион
кватернион 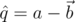 , который назовём сопряжённым к нему. Из выведенной выше формулы можно видеть, что
, который назовём сопряжённым к нему. Из выведенной выше формулы можно видеть, что  . Таким образом, мы можем ввести для кватернионов норму
. Таким образом, мы можем ввести для кватернионов норму 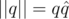 и обратный элемент
и обратный элемент 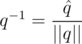 . Обратим внимание на то, что
. Обратим внимание на то, что 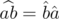 . Действительно, из формулы умножения прямо следует
. Действительно, из формулы умножения прямо следует 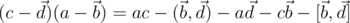 . Отсюда сразу следует, что
. Отсюда сразу следует, что 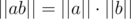 и
и 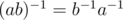 .
.
Здесь и далее будем считать векторы кватернионами с нулевой скалярной частью. Введём операцию сопряжения вектора a кватернионом g, результатом которой является вектор[1] 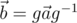 . Это равенство эквивалентно тому, что
. Это равенство эквивалентно тому, что 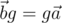 . Пусть
. Пусть 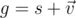 , тогда, расписывая, получаем
, тогда, расписывая, получаем 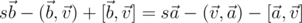 . Рассматривая отдельно скалярные и векторные части, получаем:
. Рассматривая отдельно скалярные и векторные части, получаем:
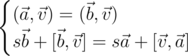
Обратим внимание, что в силу мультипликативности нормы кватернионов, нормы векторов 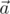 и
и 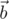 равны. Первое уравнение системы означает, что равны также их ортогональные проекции на ось
равны. Первое уравнение системы означает, что равны также их ортогональные проекции на ось 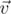 . Отсюда необходимо следует, что
. Отсюда необходимо следует, что 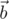 получается из
получается из 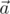 поворотом вокруг
поворотом вокруг 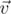 на некоторый угол. Найдём его.
на некоторый угол. Найдём его.
Будем считать, что 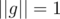 . Если это не так, отнормируем
. Если это не так, отнормируем 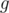 , поделив его на квадратный корень из нормы, на векторе
, поделив его на квадратный корень из нормы, на векторе 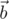 это не отразится. Теперь мы можем считать, что
это не отразится. Теперь мы можем считать, что 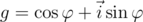 , где
, где 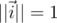 . Также пользуясь первым уравнением и вводя обозначение
. Также пользуясь первым уравнением и вводя обозначение 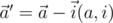 и подобное для
и подобное для 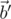 для ортогональных составляющих векторов
для ортогональных составляющих векторов 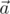 и
и 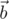 , мы можем преобразовать второе уравнение следующим образом:
, мы можем преобразовать второе уравнение следующим образом: 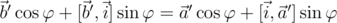 .
.
Это уравнение примечательно тем, что составлено для проекций векторов 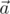 и
и 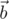 на плоскость, в которой происходит вращение. Нам остаётся лишь заметить, что
на плоскость, в которой происходит вращение. Нам остаётся лишь заметить, что 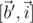 — это вектор
— это вектор 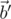 , повернутый на
, повернутый на 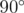 вокруг вектора
вокруг вектора 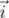 по часовой стрелке. Таким образом, первое равенство задаёт вектор
по часовой стрелке. Таким образом, первое равенство задаёт вектор 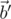 , повернутый вокруг
, повернутый вокруг 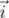 по часовой стрелке, а второе — вектор
по часовой стрелке, а второе — вектор 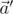 , повернутый вокруг
, повернутый вокруг 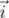 против часовой стрелки. Отсюда окончательно получаем, что вектор
против часовой стрелки. Отсюда окончательно получаем, что вектор 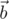 является повернутым вокруг вектора
является повернутым вокруг вектора 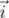 против часовой стрелки на угол
против часовой стрелки на угол 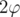 вектором
вектором 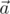 .
.
Подводя некоторый итог, мы приходим к наиболее значимому выводу этой статьи: кватернион с единичной нормой вида
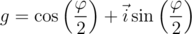 обладает тем свойством, что для любого вектора
обладает тем свойством, что для любого вектора 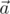 выражение
выражение 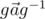 задаёт вектор
задаёт вектор 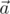 , повёрнутый вокруг
, повёрнутый вокруг 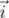 на
на 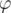 градусов против часовой стрелки.
градусов против часовой стрелки.[1] 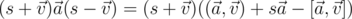 . Скалярная часть этого произведения равна
. Скалярная часть этого произведения равна 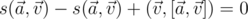 .
.







