Всем привет! Как вы уже, наверно, знаете (если не знаете — то советую узнать), в двумерной геометрии весьма удобно использовать комплексные числа для задания точек и вращений. Сейчас я хочу рассказать вам о похожей конструкции, которая позволяет эффективно работать с трёхмерным пространством.

Итак, кватернион — это гиперкомплексное число, которое может быть представлено в виде , где — действительные числа, а 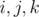— мнимые единицы, для которых имеет место тождество . Из этого тождества может быть выведена вся таблица умножения кватернионных единиц:

Стоит обратить внимание на то, что умножение мнимых единиц антикоммутативно.

Четвёрку 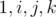можно рассматривать как ортонормированный базис в четырёхмерном линейном пространстве, а кватернионы представлять в виде , где — нормированный вектор трёхмерного линейного пространства с базисом 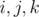.