Всем привет! Как вы уже, наверно, знаете (если не знаете — то советую узнать), в двумерной геометрии весьма удобно использовать комплексные числа для задания точек и вращений. Сейчас я хочу рассказать вам о похожей конструкции, которая позволяет эффективно работать с геометрией пространства, в частности, задавать векторы и проводить над ними линейные операции (сложение, умножение на число), считать многие известные операции над векторами и осуществлять вращения в трехмерном пространстве.

Пусть 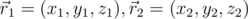— векторы в трехмерном пространстве. В статье будут использоваться следующие обозначения из аналитической геометрии:

1. Скалярное произведени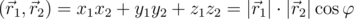е: , где 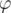— угол между векторам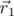и и 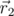в плоскости, которая их содержит, 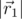— длина вектора .

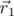2. Векторное произведени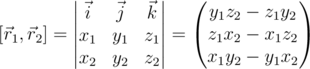е: , где 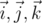— единичные вектора, направленные вдоль осе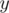й , и соответственно. В пространстве векторное произведение имеет длину 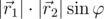и направлено перпендикулярно плоскости этих векторов таким образом, что если смотреть с вершины векторного произведения, кратчайший поворот от вектора 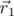к вектору 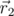происходит против часовой стрелки.

Итак, кватернион — это гиперкомплексное число, которое может быть представлено в ви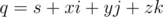де , где 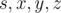— действительные числа, а 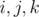— мнимые единицы. На кватернионах может быть введена операция умножения, которая задана тождеством 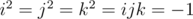. Из этого тождества может быть выведена вся таблица умножения кватернионных единиц:

Полагая кватернионное умножение дистрибутивным относительно сложения (т.е. 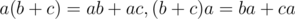), мы можем умножать кватернионы, "раскрывая скобки". Заметим, что кватернионное умножение будет ассоциативным (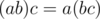), но в общем случае не коммутативным (существуют 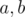такие, что ).

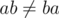Кватернионы можно представлять в ви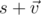де , где 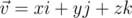— вектор трёхмерного пространства с единичными направляющими векторами 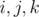. Компоненты и 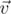называются соответственно скалярной и векторной составляющими кватерниона. Пусть у нас есть кватернионы 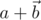и 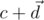. Тогда их произведение можно посчитать как 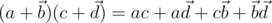. Рассмотрим подробнее умножение двух чисто векторных кватернионов.

.

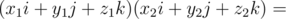
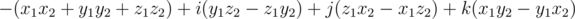Заметим, что это можно кратко переписать как 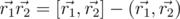. Таким образом, окончательно получаем формулу для произведения кватернионов:

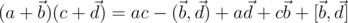
Наконец, обратим внимание, что, т.к. 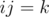, кватернион 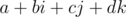может также быть задан в ви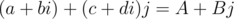де , где 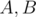— комплексные числа. Заметим, что, т.к. , имеет место 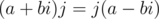или, вводя запись 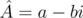: 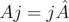. Отсюда следует, что произведение кватернионов 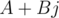и 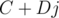может быть записано как 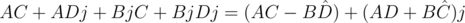. Число 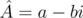, введённое выше называют сопряжённым к комплексному числу 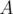. Именно эта формула для умножения кватернионов в силу своей простоты и краткости будет взята за основу в реализации кватернионов. Итак, ещё одна формула для умножения кватернионов:

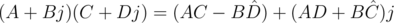
Покажем, что любой ненулевой кватернион обратим, то есть, для любого кватерниона 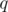существует обратный 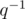такой что 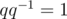. В таком случае мы сможем ввести деление как умножение на обратный элемент. По аналогии с комплексными числами можно рассмотреть для кватерниона 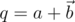кватернион 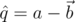, который назовём сопряжённым к нему. Из выведенной выше формулы произведения можно видеть, что 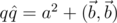. Таким образом, мы можем ввести для кватернионов норму (обобщённую длину) 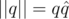и обратный элемент 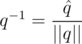. Обратим внимание на то, что 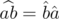. Действительно, из формулы умножения прямо следует 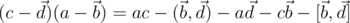. Отсюда сразу следует, что 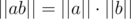и .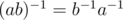

Теперь разберёмся с наиболее важным свойством кватернионов — заданием вращений трехмерного пространства. Здесь и далее будем считать векторы кватернионами с нулевой скалярной частью. Введём операцию сопряжения вектора a кватернионом g, результатом которой является вектор^[1] 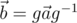. Это равенство эквивалентно тому, что 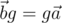. Пусть 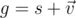, тогда, расписывая, получаем 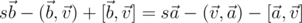. Рассматривая отдельно скалярные и векторные части, получаем:

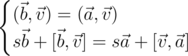
Обратим внимание, что в силу мультипликативности нормы кватернионов, нормы векторов 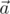и 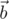равны. Первое уравнение системы означает, что равны также их ортогональные проекции на ось 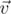. Множество концов векторов с постоянной нормой и проекцией на некоторое направление образуют окружность вокруг данного направления. Отсюда необходимо следует, что 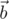получается из 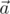поворотом вокруг 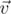на некоторый угол. Найдём его. Далее будем говорить, что вращение происходит по или против часовой стрелки в соответствии с тем, как оно выглядит, если смотреть из конца вектора, вокруг которого оно происходит.

Будем считать, что 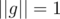. Если это не так, разделим 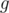на квадратный корень из его нормы, на векторе 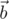это не отразится. Теперь мы можем считать, что 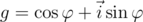, где 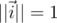. Также пользуясь первым уравнением системы и вводя обозначения 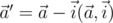и 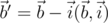, мы можем преобразовать второе уравнение следующим образом: 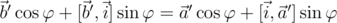. (С одной стороны мы вычли с обеих сторон 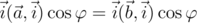, с другой, т.к. 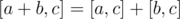имеем )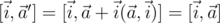

Обратим внимание на то, что 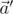и 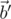лежат в одной плоскости, ортогональной вектору 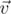, то есть, в плоскости вращения. Нам остаётся лишь заметить, что 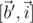— это вектор 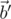, повернутый на 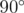вокруг вектора 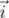по часовой стрелке. Таким образом, первое равенство задаёт вектор 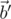, повернутый вокруг 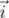по часовой стрелке на 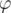, а второе — вектор 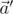, повернутый вокруг 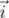против часовой стрелки на 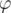. Отсюда окончательно получаем, что вектор 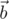является повернутым вокруг вектора 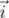против часовой стрелки на угол 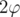вектором .

---

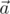Подводя некоторый итог, мы приходим к наиболее значимому выводу этой статьи: кватернион с единичной нормой вида 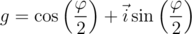обладает тем свойством, что для любого вектора 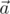выражение 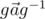задаёт вектор 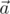, повёрнутый вокруг 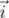на 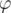градусов против часовой стрелки.

[1] 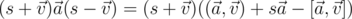. Скалярная часть этого произведения равна .

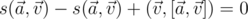Теперь приведём реализацию. Она исключительно олимпиадная и сделана с уклоном на простоту воспроизведения. Ideone: #BBOx9H

// Для начала введём обозначения для класса и его элементов, которыми мы будем пользоваться.
typedef double ftype;
typedef complex<ftype> point;
typedef complex<point> quater;
#define qA real()
#define qB imag()
#define qs qA.real()
#define qx qA.imag()
#define qy qB.real()
#define qz qB.imag()

// Умножение по формулам для комплексных чисел.
quater operator * (quater a, quater b)
{
    return {{a.qA * b.qA - a.qB * conj(b.qB)},
            {a.qA * b.qB + a.qB * conj(b.qA)}};
}

// Сопряжённый элемент.
quater conj(quater a)
{
    return {conj(a.qA), - a.qB};
}

// Кватернионная норма.
ftype norm(quater a)
{
    return (a * conj(a)).qs;
}

// Длина. 
ftype abs(quater a)
{
    return sqrt(norm(a));
}

// Деление с помощью обратного элемента.
quater operator / (quater a, quater b)
{
    return a * conj(b) / point(norm(b));
}

// Кватернион по координатам вектора.
quater vec(ftype x, ftype y, ftype z)
{
    return {{0, x}, {y, z}};
}

// Векторная часть кватерниона.
quater vec(quater a)
{
    return a -= a.qs;
}

// Скалярное произведение.
ftype dot(quater a, quater b)
{
    return -(a * b).qs;
}

// Векторное произведение.
quater cross(quater a, quater b)
{
    return vec(a * b);
}

// Смешанное произведение.
ftype mix(quater a, quater b, quater c)
{
    return dot(a, cross(b, c));
}

// Сопряжение вектора a кватернионом g.
quater conj(quater a, quater g)
{
    return g * a / g;
}

// Кватернион, задающий вращение вокруг i на phi
quater rotation(quater i, ftype phi)
{
    return point(cos(phi / 2)) + i * point(sin(phi / 2));
}

// Вращать a вокруг i на phi по часовой стрелке.
quater rotate(quater a, quater i, ftype phi)
{
    return conj(a, rotation(i, phi));
}

// Кватернион, задающий вращение от a к b по минимальному углу.
quater min_rotation(quater a, quater b)
{
    a /= abs(a);
    b /= abs(b);
    return -conj(a * (a + b));
}
// Угол вращения, который задаёт кватернион.
ftype get_angle(quater a)
{
    a /= abs(a);
    return 2 * acos(a.qs);
}

Недостатки:

1. complex<complex<double>> — unspecified behavior. В приведённой реализации из класса без перегрузки используются только линейные операции и это должно работать в любой разумной реализации complex<>, но всё же стоит помнить об этой особенности.

2. Наиболее простой способ умножить кватернион на вещественное число в такой реализации — сперва привести это число к complex<double>.

P.S. С моей точки зрения, must-have набор для 3D-геометрии выглядит именно так, а остальное уже из него выводится. Если хотите видеть здесь какие-нибудь ещё функции трехмерной геометрии, пишите в комментариях. И вообще если есть какие-нибудь советы, жалобы или задачи, которые было бы неплохо решить кватернионами, пишите их :)